Question

Cho điểm D nằm bên ngoài đường tròn (o) từ D kẻ hai tiếp tuyến DB,DC với đường tròn đó (B,C là các tiếp điểm) Gọi H là trung điểm của DB , đường thẳng HC cắt đường tròn (o) tại M a) cm tgDBOC b) BH² = HM.HC

Answer 1

a.

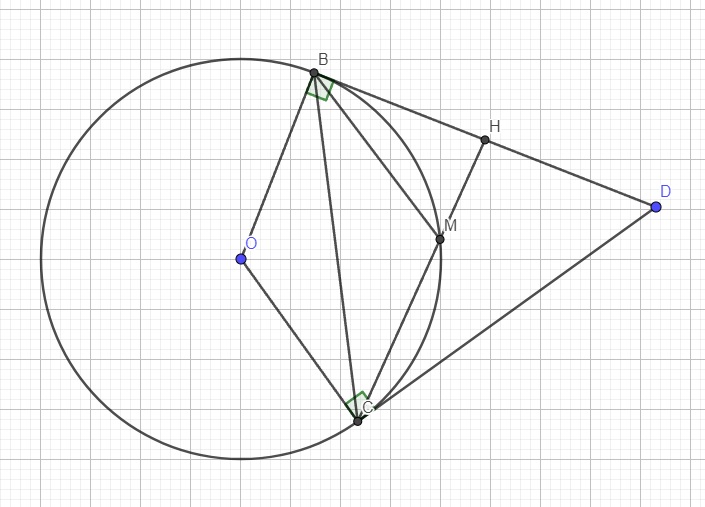
Do DB, DC là tiếp tuyến của (O) \(\Rightarrow\widehat{DBO}=\widehat{DCO}=90^0\)

\(\Rightarrow\) B và C cùng nhìn OD dưới 1 góc vuông nên DBOC nội tiếp đường tròn đường kính OD

b.

Xét hai tam giác CBH và BMH có:

\(\left\{{}\begin{matrix}\widehat{BHM}-chung\\\widehat{BCH}=\widehat{MBH}\left(\text{cùng chắn BM}\right)\end{matrix}\right.\) 

\(\Rightarrow\Delta CBH\sim\Delta BMH\left(g.g\right)\)

\(\Rightarrow\dfrac{BH}{HM}=\dfrac{HC}{BH}\Rightarrow BH^2=HM.HC\)

Answer 2

Answer 3

SỬA LẠI GIÚP MÌNH TỪ TÂM A THÀNH TÂM O NHA:

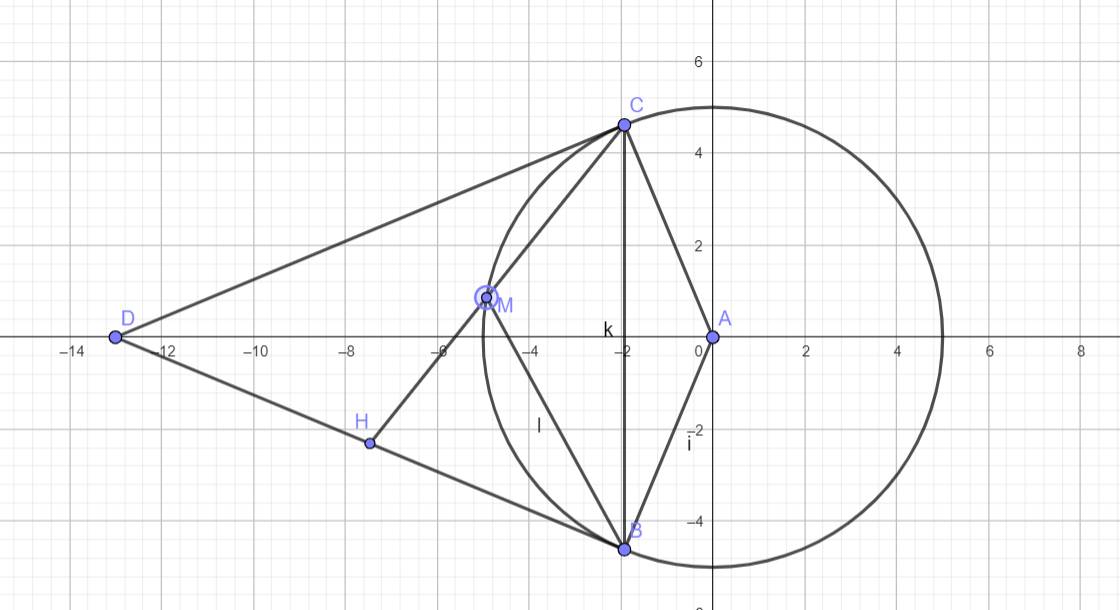
a) ta có:

góc DCO = 90(DC là tiếp tuyến )

góc DBO = 90(DB là tiếp tuyến )

DCO + DBO = 180(vì B đối C)

⇒ tứ giác DBOC nội tiếp