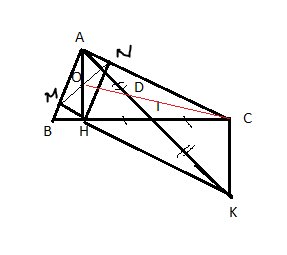
Cho \(\Delta ABC\) vuông tại A có \(AB< AC,\) đường cao AH. Từ H kẻ \(HM\perp AB\left(M\in AB\right),\) kẻ \(HN\perp AC\left(N\in AC\right)\). Gọi I là trung điểm của HC, lấy K trên tia AI sao cho I là trung điểm của AK.
a. Cminh: tứ giác AHKC là hình bình hành.
b. Biết MN cắt AH tại O. Cminh: \(MH//AC;\widehat{OMH}=\widehat{HKC.}\)
c. Gọi D là giao điểm của CO và AK. Cminh: \(AK=3AD.\)
a, Xét tứ giác AHKC có: I là trung điểm của AK và HC, đồng thời AK cắt HC tại I
⇒ Tứ giác AHKC là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường) (dpcm)
b, Do tứ giác AHKC là hình bình hành ⇒ \(\widehat{HKC}=\widehat{HAC}\) (tinh chat hinh binh hanh) (1)
Xét tứ giác AMHN có:
\(\widehat{MAN}=90^o\left(doAB\perp AC\right)\)
\(\widehat{AMH}=90^o\left(doAM\perp HM\right)\)
\(\widehat{ANH}=90^o\left(doAN\perp HN\right)\)
⇒ Tứ giác AMHN là hình chữ nhật ⇒ MH = AN, \(\widehat{MHN}=\widehat{ANH}\left(=90^o\right)\) (tính chất hình chữ nhật)
Xét ΔMHN và ΔANH có:
MH = AN
\(\widehat{MHN}=\widehat{ANH}\)
HN chung
⇒ ΔMHN = ΔANH (c-g-c) ⇒ \(\widehat{NMH}=\widehat{HAN}hay\widehat{OMH}=\widehat{HAC}\) ( 2 goc tuong ung) (2)
Từ (1) và (2) ⇒ \(\widehat{OMH}=\widehat{HKC}\left(dpcm\right)\)
c, Do tứ giác AMHN là hình chữ nhật có hai đường chéo MN và AH cắt nhau tại O
⇒ O là giao điểm của hai đường chéo ⇒ O là trung điểm của AH
Xét ΔAHC có: I là trung điểm của HC, O là trung điểm của AH, CO cắt AI tại D
⇒ D là trọng tâm ΔAHC
⇒ \(AD=\dfrac{2}{3}AI\) (tinh chat trong tam tam giac)
Lại có: 2AI = AK (do I là trung điểm của AK)
Như vậy, \(AD=\dfrac{AK}{3}\Rightarrow3AD=AK\left(dpcm\right)\)













