Question

cho ΔABC vuông tại A có đường cao AH

a) chứng minh ΔABC đồng dạng ΔHBA

b) tính độ dài cạnh AB nếu biết BC = 9cm; BH = 4cm

c) phân giác BD của góc ABC (D thuộc AC) cắt AH tại E. chứng minh \(\dfrac{HE}{AE}=\dfrac{AD}{CD}\)

Answer 1

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

\(\widehat{ABC}\) chung

Do đó: ΔABC~ΔHBA

b: ΔABC~ΔHBA

=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\left(1\right)\)

=>\(BA^2=BH\cdot BC=4\cdot9=36=6^2\)

=>BA=6(cm)

c: Xét ΔBAH có BE là phân giác

nên \(\dfrac{BA}{BH}=\dfrac{EA}{EH}\left(2\right)\)

Xét ΔBAC có BD là phân giác

nên \(\dfrac{BC}{BA}=\dfrac{DC}{DA}\left(3\right)\)

Từ (1),(2),(3) suy ra \(\dfrac{EA}{EH}=\dfrac{DC}{DA}\)

=>\(\dfrac{EH}{EA}=\dfrac{AD}{DC}\)

Answer 2

  

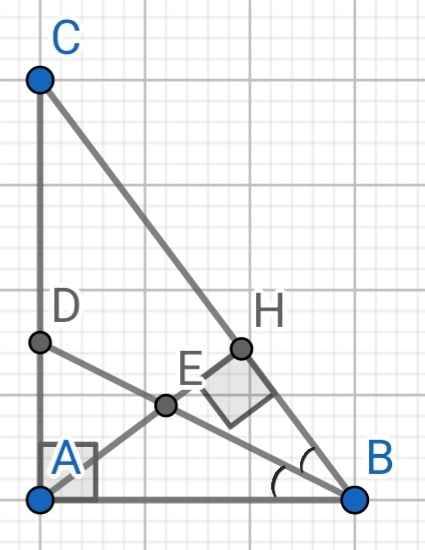
a) Xét hai tam giác vuông: ∆ABC và ∆HBA có:

∠B chung

⇒ ∆ABC ∽ ∆HBA (g-g)

b) Do ∆ABC ∽ ∆HBA (cmt)

⇒ AB/BH = BC/AB

⇒ AB² = BH.BC

= 4.9

= 36

⇒ AB = 6 (cm)

c) ∆ABC có:

BD là đường phân giác (gt)

⇒ AD/CD = AB/BC

Do BD là tia phân giác của ∠ABC (gt)

⇒ BE là tia phân giác của ∠ABH

⇒ BE là đường phân giác của ∆ABH

∆ABH có:

BE là đường phân giác (cmt)

⇒ HE/AE = BH/AB

Do AB/BH = BC/AB (cmt)

⇒ BH/AB = AB/BC

Mà HE/AE = BH/AB (cmt)

⇒ HE/AE = AB/BC

Mà AD/CD = AB/BC (cmt)

⇒ HE/AE = AD/CD