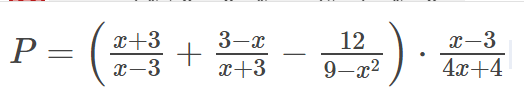Question

Cho biểu thức:

a, Rút gọn P.

b, Tính giá trị của P tại x = -2.

\[ P = \left( \frac{x+3}{x-3} + \frac{3-x}{x+3} - \frac{12}{9-x^2} \right) \cdot \frac{x-3}{4x+4} \]

Answer 1

a: ĐKXĐ: \(x\notin\left\{3;-3;-1\right\}\)

\(P=\left(\dfrac{x+3}{x-3}+\dfrac{3-x}{x+3}-\dfrac{12}{9-x^2}\right)\cdot\dfrac{x-3}{4x+4}\)

\(=\dfrac{\left(x+3\right)^2-\left(x-3\right)^2+12}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x-3}{4\left(x+1\right)}\)

\(=\dfrac{x^2+6x+9-x^2+6x-9+12}{\left(x+3\right)}\cdot\dfrac{1}{4\left(x+1\right)}\)

\(=\dfrac{12x+12}{4x+4}\cdot\dfrac{1}{x+3}=\dfrac{3}{x+3}\)

b: Khi x=-2 thì \(P=\dfrac{3}{-2+3}=\dfrac{3}{1}=3\)

Answer 2

`a, P=( (x+3)/(x-3) + (3-x)/(x+3) - 12/(9-x^2)) * (x-3)/(4x+4)`

`=( ((x+3)^2)/((x-3)(x+3)) - ((x-3)^2)/(x-3)(x+3))+12/((x-3)(x+3)) ) * (x-3)/(4(x+1))`

`=(x^2+6x+9 - x^2 +6x-9+12)/((x-3)(x+3)) * (x-3)/(4(x+1))`

`=(12x+12)/((x-3)(x+3)) * (x-3)/(4(x+1))`

`=(12(x+1))/((x-3)(x+3)) * (x-3)/(4(x+1))`

`= 3/(x+3)`

`b,` Tại `x=-2` ta có :

`P=3/(x+3)=3/(-2+3)=3/1=3`

`#NgCTh#`