Phương pháp:
Sử dụng phương pháp tích phân từng phần để tìm

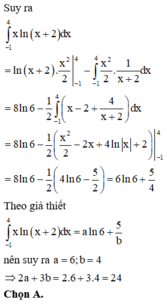

Phương pháp:
Sử dụng phương pháp tích phân từng phần để tìm

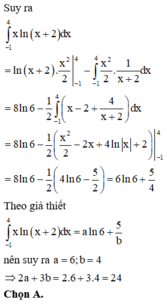

Cho tích phân I = ∫ 0 1 ( x + 2 ) ln ( x + 1 ) d x = a l n 2 − 7 b trong đó a, b là các số nguyên dương. Tổng a + b 2 bằng
A. 8
B. 16
C. 12
D. 20
Cho hai số thực không âm x,y ≤ 1. Biết P = l n ( 1 + x 2 ) ( 1 + y 2 ) + 8 17 ( x + y ) 2 có giá trị nhỏ nhất là - a b + 2 ln c d trong đó a, b, c, d là số tự nhiên thỏa mãn ước chung của (a,b) = (c,d) = 1. Giá trị của a+b+c+d là
A. 406
B. 56
C. 39
D. 405
Biết ∫ 1 3 2 + ln ( x + 3 ) ( x + 1 ) 2 dx =a ln2+b ln3+c (a,b,c∈Q). Giá trị 3a-b+2c bằng
A. 7.
B. 0.
C. -2.
D. -11/2
Cho ∫ 1 2 6 x x + 1 + x + 1 d x = a + b - c với a,b,c là các số nguyên dương. Giá trị biểu thức a+b+c bằng
A. 247.
B. 236.
C. 246.
D. 237.
Cho ∫ 1 e ln x ( l n x + x + 1 ) 2 d x = a e - 2 b e + 4 , với a,b là các số nguyên dương. Giá trị của biểu thức b-a bằng
A. 1.
B. 3.
A. -1.
D. -3.
Cho ∫ 1 e ln x ln x + x + 1 2 d x = a e - 2 b e + 4 với a,b là các số nguyên dương. Giá trị của biểu thức b - a bằng
A. 6.
B. 9.
C. 12.
D. 18.
Cho ∫ 1 e ln x ln x + x + 1 2 d x = a e - 2 b e + 4 với a,b là các số nguyên dương. Giá trị của biểu thức b - a bằng
A. 1.
B. 3.
C. - 1
D. - 3
Cho ∫ 0 9 16 1 x + 1 + x + 1 d x = a - b ln 2 c với a,b,c là các số nguyên dương và a/c tối giản. Giá trị của biểu thức a+b+c bằng
A. 43.
B. 48.
C. 88.
D. 33.
Cho ∫ 1 e 1 x + ln x x ln x + 2 2 d x = a ln 3 + b ln 2 + c 3 với a , b , c ∈ ℤ . Giá trị của a 2 + b 2 + c 2 bằng
A. 3
B. 6
C. 9
D. 12
Cho ∫ 1 3 1 + 1 x 2 d x = a - b + ln c + d e với c nguyên dương và a,b,d,e là các số nguyên tố. Giá trị của biểu thức a+b+c+d+e bằng
A. 10
B. 14
C. 24
D. 17