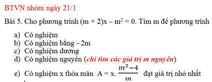a: \(Q=\dfrac{2x^2-4x+x-3-6}{\left(x-3\right)\left(x-2\right)}\cdot\dfrac{x-2}{x^2+1}=\dfrac{2x^2-3x-9}{x-3}\cdot\dfrac{1}{x^2+1}\)
\(=\dfrac{2x^2-6x+3x-9}{x-3}\cdot\dfrac{1}{x^2+1}=\dfrac{2x+3}{x^2+1}\)
b: Để Q>0 thì 2x+3>0
hay x>-3/2
Bài 2:
a) Q=(\(\dfrac{2x}{x-3}-\dfrac{1}{2-x}-\dfrac{6}{x^2-5x+6}\)):\(\dfrac{x^2+1}{x-2}\)
=(\(\dfrac{2x}{x-3}+\dfrac{1}{x-2}-\dfrac{6}{x^2-2x-3x+6}\)):\(\dfrac{x^2+1}{x-2}\)
=[\(\dfrac{2x}{x-3}+\dfrac{1}{x-2}-\dfrac{6}{x\left(x-2\right)-3\left(x-2\right)}\)]:\(\dfrac{x^2+1}{x-2}\)
=\(\dfrac{2x\left(x-2\right)+x-3-6}{\left(x-2\right)\left(x-3\right)}\):\(\dfrac{x^2+1}{x-2}\)
=\(\dfrac{2x^2-4x+x-9}{\left(x-2\right)\left(x-3\right)}\):\(\dfrac{x^2+1}{x-2}\)
=\(\dfrac{2x^2-3x-9}{\left(x-2\right)\left(x-3\right)}\):\(\dfrac{x^2+1}{x-2}\)
=\(\dfrac{2x^2-6x+3x-9}{\left(x-2\right)\left(x-3\right)}\):\(\dfrac{x^2+1}{x-2}\)
=\(\dfrac{2x\left(x-3\right)+3\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}\):\(\dfrac{x^2+1}{x-2}\)
=\(\dfrac{\left(x-3\right)\left(2x+3\right)}{\left(x-2\right)\left(x-3\right)}\):\(\dfrac{x^2+1}{x-2}\)
=\(\dfrac{\left(2x+3\right)}{\left(x-2\right)}\):\(\dfrac{x^2+1}{x-2}\)
=\(\dfrac{2x+3}{x^2+1}\)
Để \(\dfrac{1}{Q}\)=\(\dfrac{x^2+1}{2x+3}\)là số nguyên thì x2+1 chia hết cho 2x+3
x2 +1 2x+3
x2+\(\dfrac{3}{2}\)x \(\dfrac{1}{2}\)x-\(\dfrac{3}{4}\)
______
-\(\dfrac{3}{2}\)x+1
-\(\dfrac{3}{2}\)x-\(\dfrac{9}{4}\)
____________
\(\dfrac{13}{4}\)
=>\(\dfrac{1}{Q}\)không nguyên

 ạ vì mình ko hiểu ạ
ạ vì mình ko hiểu ạ