c: Gọi \(\left(d_1\right):y=ax+b\left(a< >0\right)\)
Vì (d1) đi qua M(0;-1) nên thay x=0 và y=-1 vào (d1), ta được:
\(a\cdot0+b=-1\)
=>b=-1
=>(d1): y=ax-1
Phương trình hoành độ giao điểm là:
\(x^2-ax+1=0\)
\(\text{Δ}=\left(-a\right)^2-4\cdot1\cdot1=a^2-4\)
Để (d1) tiếp xúc với (P) thì \(a^2-4=0\)
=>a=2 hoặc a=-2
Vậy: (d1); y=2x-1 hoặc y=-2x-1
`c)` Gọi ptr đường thẳng `(d1)` có dạng: `y=ax+b` `(a \ne 0)`
Vì `M(0;-1) in (d1)=>b=-1`
Xét ptr hoành độ của `(d1)` và `(P)` có:
`x^2=ax+b`
`<=>x^2-ax-b=0` `(1)`
`(d1)` tiếp xúc với `(P)<=>` Ptr `(1)` có nghiệm kép
`=>\Delta=0`
`<=>(-a)^2-4.(-b)=0`
`<=>a^2+4b=0`
Mà `b=-1`
`=>a^2-4=0`
`<=>a=+-2` (t/m)
Vậy ptr đường thẳng `(d1)` có dạng: `y=2x-1` hoặc `y=-2x-1`

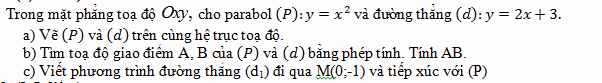














 Ai chỉ em với câu c với khó quá huhu
Ai chỉ em với câu c với khó quá huhu 

