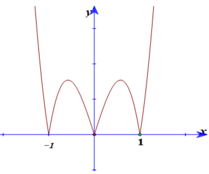
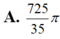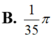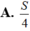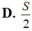Câu 42: Xét hàm số \(f\left(x\right)=ax^3+bx^2+cx+d\) \((a,b,c,d \in \mathbb{R}, a > 0)\) có hai điểm cực trị \(x_1,x_2 \) (với \(x_1 < x_2\)) thỏa mãn \(x_1+x_2=0.\) Hình phẳng giới hạn bởi đường \(y = f'(x)f''(x)\) và trục hoành có diện tích bằng \(\dfrac{9}{4}\). Biết \(\displaystyle \int_{x_1}^{x_2}\)\(\dfrac{f'\left(x\right)}{3^x+1}dx=-\dfrac{7}{2}\) , giá trị của \(\displaystyle \int_{0}^{x_2}(x+2)f''(x)dx\) thuộc khoảng nào dưới đây?
A. (6; 7). B. (0; 1). C. (-1; 0). D. (-7; -6).
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho f(x) là hàm số bậc 4 thỏa mãn \(f\left(0\right)=\dfrac{-1}{\ln2}\). Hàm số \(f'\left(x\right)\) có bảng biến thiên như sau:
Hàm số \(g\left(x\right)=\left|f\left(-x^2\right)-x^2+\dfrac{2^{x^2}}{\ln2}\right|\) có bao nhiêu điểm cực trị?
A. 3
B.2
C.4
D.5
Cho hàm số \(f\left(x\right)\) có đạo hàm bằng \(f'\left(x\right)=x^2\left(x-1\right)^3\left(x-2\right)\) . Số điểm cực trị của hàm số \(f\left(x\right)\) bằng:
A.0 B.1 C.2 D.3
Cho hàm số \(y=f\left(x\right)\) là hàm số bậc bốn thỏa mãn \(f\left(0\right)=0\) .Hàm số \(y=f'\left(x\right)\) có bảng biến thiên như sau:
Hàm số \(g\left(x\right)=\left|f\left(x^2\right)-x^2\right|\) có bao nhiêu điểm cực trị?
A.1
B.3
C.5
D.7
Cho hàm số y=f(x)= a x 3 + b x 2 + c x + d , ( a , b , c , d ∈ R , a khác 0) có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y= f ' ( x ) cho bởi hình vẽ dưới đây. Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giời hạn bởi đồ thị (C) và trục hoành xung quanh trục hoành Ox
Cho f ( x ) = x 3 + a x 2 + b x + c và g ( x ) = f ( d x + e ) với a , b , c , d , e ∈ ℝ có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=f(x) Diện tích hình phẳng giới hạn bởi hai đường congy=f(x) và y=g(x) gần nhất với kết quả nào dưới đây?
A. 4,5
B. 4,25
C. 3,63
D. 3,67
Xét các khẳng định sau:
(1) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 1 điểm chung.
(2) Nếu hàm số y=f(x) xác định trên R thỏa mãn f(-1).f(0)<0 và f(0).f(1)<0 thì đồ thị của hàm số y=f(x) và trục hoành có ít nhất 2 điểm chung.
Phát biểu nào sau đây đúng?
A. Khẳng định 
đúng và khẳng định 
sai.
B. Khẳng định 
sai và khẳng định 
đúng.
C. Khẳng định 
sai và khẳng định 
sai.
D. Khẳng định 
đúng và khẳng định 
đúng.
Cho hàm số bậc 4 y = f(x) có đồ thị như hình vẽ bên. Biết hàm số y = f(x) đạt cực trị tại các điểm x1,x2,x3 thỏa mãn x3 = x1+2, f(x1) + f(x3) +\(\dfrac{2}{3}\)f(x2) = 0 và (C) nhận đường thẳng x = x2 làm trục đối xứng. Gọi S1,S2,S3,S4 là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số \(\dfrac{S_1+S_2}{S_3+S_4}\) gần với kết quả nào nhất :
Cho hàm số y= f( x) =ax4+ bx2+ c ( a> 0) có đồ thị (C), đồ thị hàm số y= f’(x). Đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
A. 7 15
B. 8 15
C. 14 15
D. 16 15
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
