36:
A=[3;+\(\infty\)); B=(0;4)
A\(\cap\)B=[3;4)
A\(\cup\)B=(0;+\(\infty\))
A\B=[4;+\(\infty\))
B\A=(0;3)
\(A\cap B=\) `[3;4)`
\(A\cup B=\) `(0;+∞)`
`A`\`B = [4;+∞)`
`B`\`A = (0;3)`
36:
A=[3;+\(\infty\)); B=(0;4)
A\(\cap\)B=[3;4)
A\(\cup\)B=(0;+\(\infty\))
A\B=[4;+\(\infty\))
B\A=(0;3)
\(A\cap B=\) `[3;4)`
\(A\cup B=\) `(0;+∞)`
`A`\`B = [4;+∞)`
`B`\`A = (0;3)`
Câu 10. Tính bằng cách thuận tiện nhất:
A = (36 + 54) × 7 + 7 × 9 + 7
Cho a, b, c là ba số thực thỏa mãn điều kiện a 3 > 36 và abc = 1
Xét tam thức bậc hai
![]()
Từ câu a) suy ra
![]()
Câu 36. Đồ thị hàm số y={\(\dfrac{2x+1}{x^2-3}\) \(\dfrac{khix\le2}{khix>2}\)đi qua tọa độ có điểm
A.
(0;1)
B.
(−3;0)
C.
(0;3)
D.
(0; 3− )
câu 23:Elip có hai đỉnh là -3,0;3,0 và có hai tiêu điểm là (-1,0);(1,0).Phương trình chính tắc của elip là :A.x2/9+y2/1=1,B.x2/8+y2/9=1,c.x2/36+y2/8=1,D.x2/24+y2/16=
Câu 36. Cho các tập hợp khác rỗng [ m−1; m+3 /2 ] và B=(âm vô cùng ; -3) hợp [3;dương vô cùng). Gọi S là tập hợp các giá nguyên dương của m để A giao B ≠ ∅ . Tìm số tập hợp con của S .
Câu 35. Cho hàm số f(x) ={\(\left|\dfrac{-2\left(x-3\right)}{\sqrt{x^2}-1}\right|\) \(\dfrac{-1\le x< 1}{x\ge1}\) Gía trị của f(-1), f(1) lần lượt là.
Câu 36. Đồ thị hàm số y={\(\dfrac{2x+1}{x^2-3}\dfrac{khix\le2}{khix>2}\) đi qua điểm có tọa độ là.
Câu 37. Cho hàm số y={\(\dfrac{-2x+1khix\le-3}{\dfrac{x+7}{2}khix>-3}\) Biết f(x0) = 5 thì x0 là:
Câu 38. Hàm số y=\(\dfrac{x-2}{\left(x-2\right)\left(x-1\right)}điểm\) nào thuộc đồ thị.
Kết quả bài kiểm tra môn Toán của 36 học sinh được cho trong mẫu số liệu sau:
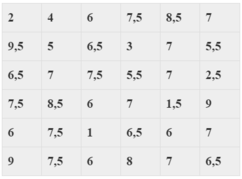
a) Lập bảng phân bố tần số và tần suất ghép lớp ( chính xác đến hàng phần trăm) sử dụng 5 lớp sau: [0;2), [2;4), [4;6), [6;8), [8;10)
b) Vẽ biểu đồ tần suất hình quạt thể hiện bảng phân bố ở câu a).
Câu 35. Cho hàm số f(x) ={∣∣∣−2(x−3)√x2−1∣∣∣|−2(x−3)x2−1| −1≤x<1x≥1−1≤x<1x≥1 Gía trị của f(-1), f(1) lần lượt là.
Câu 36. Đồ thị hàm số y={2x+1x2−3khix≤2khix>22x+1x2−3khix≤2khix>2 đi qua điểm có tọa độ là.
Câu 37. Cho hàm số y={−2x+1khix≤−3x+72khix>−3−2x+1khix≤−3x+72khix>−3 Biết f(x0) = 5 thì x0 là:
Câu 38. Hàm số y=x−2(x−2)(x−1)điểmx−2(x−2)(x−1)điểm nào thuộc đồ thị.
Câu 35. Cho hàm số f(x) ={∣∣∣−2(x−3)√x2−1∣∣∣|−2(x−3)x2−1| −1≤x<1x≥1−1≤x<1x≥1 Gía trị của f(-1), f(1) lần lượt là.
Câu 36. Đồ thị hàm số y={2x+1x2−3khix≤2khix>22x+1x2−3khix≤2khix>2 đi qua điểm có tọa độ là.
Câu 37. Cho hàm số y={−2x+1khix≤−3x+72khix>−3−2x+1khix≤−3x+72khix>−3 Biết f(x0) = 5 thì x0 là:
Câu 38. Hàm số y=x−2(x−2)(x−1)điểmx−2(x−2)(x−1)điểm nào thuộc đồ thị.
Câu 35. Cho hàm số f(x) ={∣∣∣−2(x−3)√x2−1∣∣∣|−2(x−3)x2−1| −1≤x<1x≥1−1≤x<1x≥1 Gía trị của f(-1), f(1) lần lượt là.
Câu 36. Đồ thị hàm số y={2x+1x2−3khix≤2khix>22x+1x2−3khix≤2khix>2 đi qua điểm có tọa độ là.
Câu 37. Cho hàm số y={−2x+1khix≤−3x+72khix>−3−2x+1khix≤−3x+72khix>−3 Biết f(x0) = 5 thì x0 là:
Câu 38. Hàm số y=x−2(x−2)(x−1)điểmx−2(x−2)(x−1)điểm nào thuộc đồ thị.