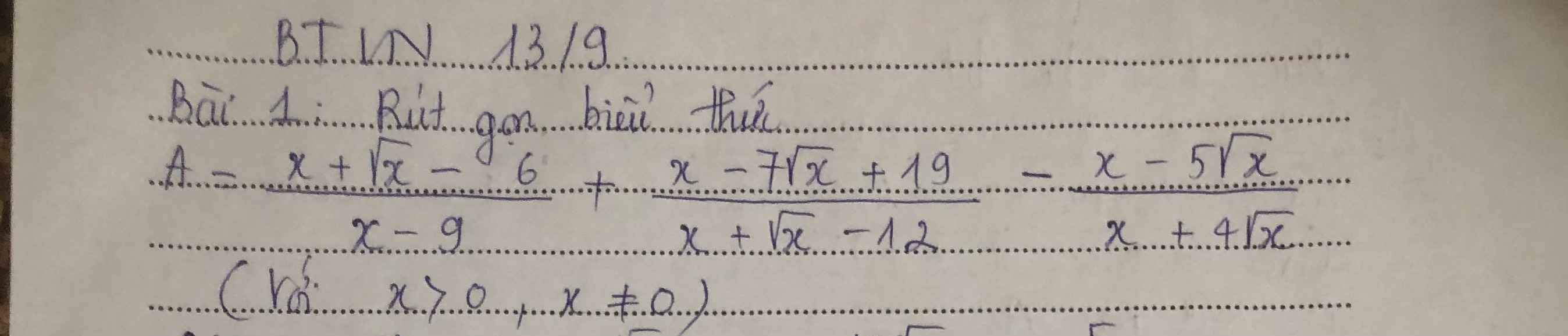\(A=\dfrac{x+\sqrt{x}-6}{x-9}+\dfrac{x-7\sqrt{x}+19}{x+\sqrt{x}-12}-\dfrac{x-5\sqrt{x}}{x+4\sqrt{x}}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)+3\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{x-7\sqrt{x}+19}{\sqrt{x}\left(\sqrt{x}-3\right)+4\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-5\right)}{\sqrt{x}\left(\sqrt{x}+4\right)}\\ =\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{x-7\sqrt{x}+19}{\left(\sqrt{x}+4\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}-5}{\sqrt{x}+4}\\ =\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+4\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+4\right)}+\dfrac{x-7\sqrt{x}+19}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+4\right)}-\dfrac{\left(\sqrt{x}-5\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+4\right)}\\ =\dfrac{x-2\sqrt{x}+4\sqrt{x}-8+x-7\sqrt{x}+19-x+5\sqrt{x}+3\sqrt{x}-15}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+4\right)}\\ =\dfrac{x+3\sqrt{x}-4}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+4\right)}\\ =\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+4\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+4\right)}\\ =\dfrac{\sqrt{x}-1}{\sqrt{x}-3}\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Tìm m nguyên để 3m3 + 2m2 + 3m + 2 là một số chính phương.
Anybody can help me please!
I will tick 5 star for noone help me
\(A=\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+...+\frac{1}{\sqrt{2004}+\sqrt{2005}}\)
giúp mình với NHANH NHANH cần gấp nhà bạn!!!!@!!!!@@!!!!@
CAN YOU HELP ME?????
help me,me cần gấp ạ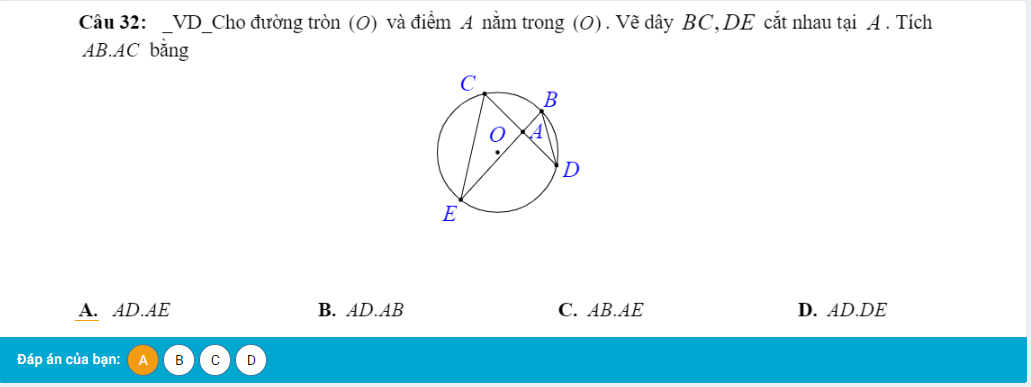
Help me với mn ơi
Giai pt giúp me
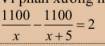
help me!!!!!
Đọc tiếp
help me!!!!!
Help me!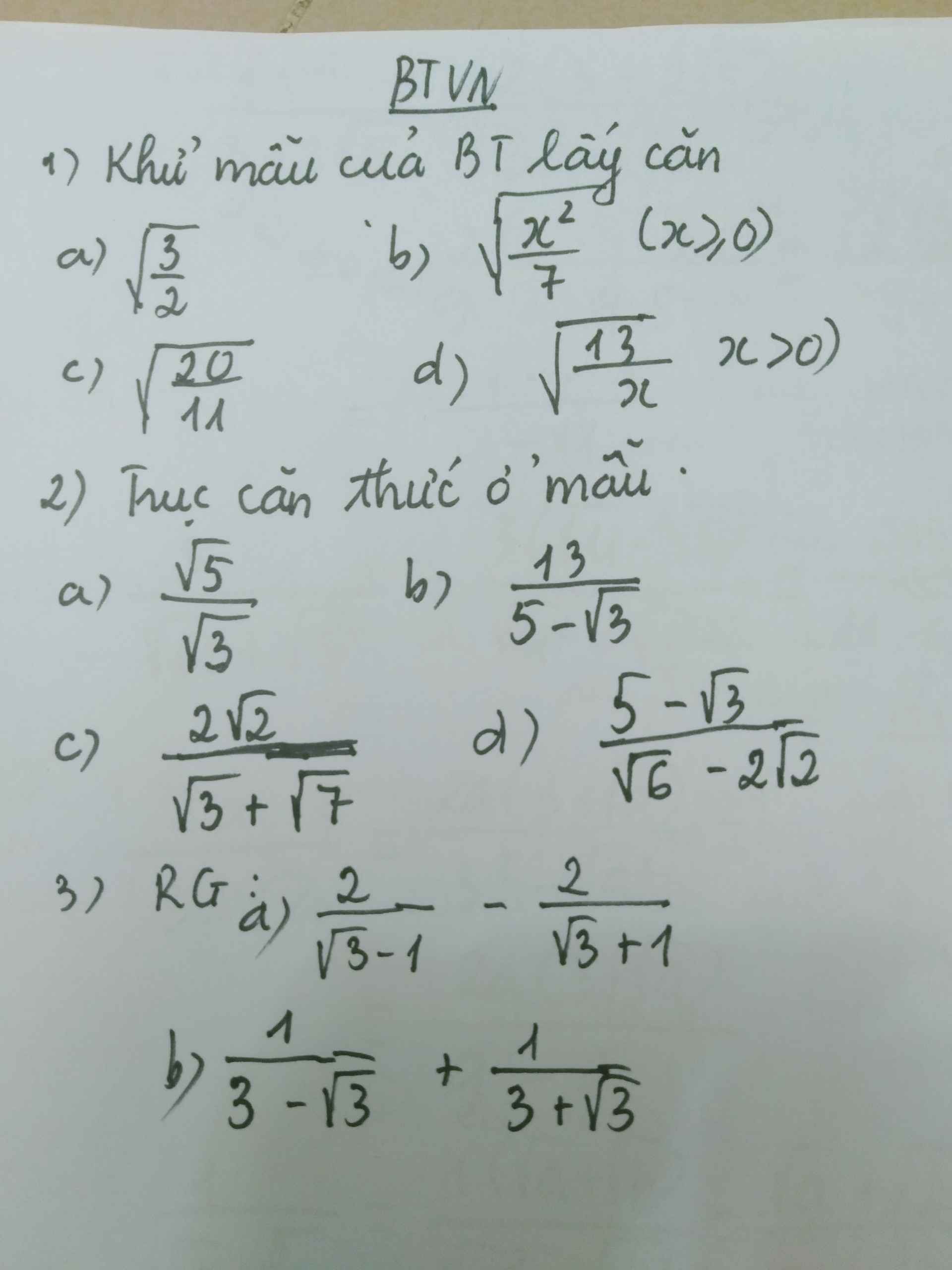
Help me!
 HELP ME
HELP ME

HELP ME
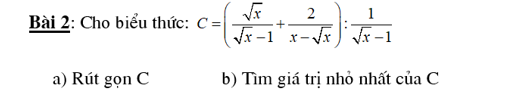
Help me