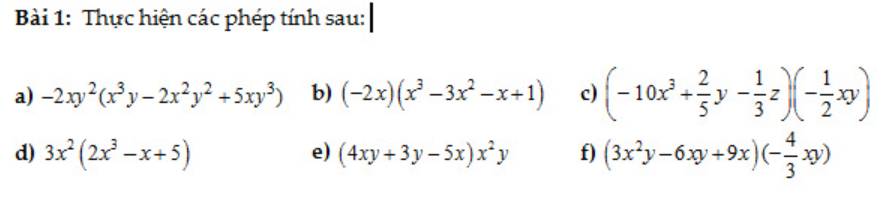a) \(-2xy^2\left(x^3y-2x^2y^2-5xy^3\right)\)
\(=-2x^4y^3+4x^3y^4+10x^2y^5\)
b) \(\left(-2x\right)\left(x^3-3x^2-x+1\right)\)
\(=-2x^4+6x^3+2x^2-2x\)
c) \(\left(-10x^3-\dfrac{2}{5}y-\dfrac{1}{3}z\right)\left(-\dfrac{1}{2}xy\right)\)
\(=5x^4y+\dfrac{1}{5}xy^2+\dfrac{1}{6}xyz\)
d) \(3x^2\left(2x^3-x+5\right)\)
\(=6x^5-3x^3+15x^2\)
e) \(\left(4xy+3y-5x\right)x^2y\)
\(=4x^3y^2+3x^2y^2-5x^3y\)
f) \(\left(3x^2y-6xy+9x\right)\left(-\dfrac{4}{3}xy\right)\)
\(=-4x^3y^2+8x^2y^2-12x^2y\)
`@` `\text {Ans}`
`\downarrow`
`a)`
\(-2xy^2(x^3y-2x^2y^2+5xy^3)\)
`= (-2xy^2)(x^3y) + (-2xy^2)(-2x^2y^2)+(-2xy^2)(5xy^3)`
`=`\(-2x^4y^3+4x^3y^4-10x^2y^5\)
`b)`
\((-2x)(x^3-3x^2-x+1)\)
`= (-2x)(x^3) + (-2x)(-3x^2) + (-2x)(-x) + (-2x)`
`= -2x^4 + 6x^3 + 2x^2 - 2x`
`c)`
\(\left(-10x^3+\dfrac{2}{5}y-\dfrac{1}{3}z\right)\left(-\dfrac{1}{2}xy\right)\)
`=`\(-10x^3\left(-\dfrac{1}{2}xy\right)+\dfrac{2}{5}y\left(-\dfrac{1}{2}xy\right)-\dfrac{1}{3}z\left(-\dfrac{1}{2}xy\right)\)
`=`\(5x^4y-\dfrac{1}{5}xy^2+\dfrac{1}{6}xyz\)
`d)`
\(3x^2(2x^3-x+5)\)
`= 3x^2*2x^3 + 3x^2*(-x) + 3x^2*5`
`= 6x^5 - 3x^3 + 15x^2`
`e)`
\((4xy+3y-5x)x^2y\)
`=`\(4xy\cdot x^2y+3y\cdot x^2y-5x\cdot x^2y\)
`=`\(4x^3y^2+3x^2y^2-5x^3y\)
`f)`
\(\left(3x^2y-6xy+9x\right)\left(-\dfrac{4}{3}xy\right)\)
`=`\(3x^2y\cdot\left(-\dfrac{4}{3}xy\right)-6xy\cdot\left(-\dfrac{4}{3}xy\right)+9x\left(-\dfrac{4}{3}xy\right)\)
`=`\(-4x^3y^2+8x^2y^2-12x^2y\)
`\text {#KaizuulvG}`