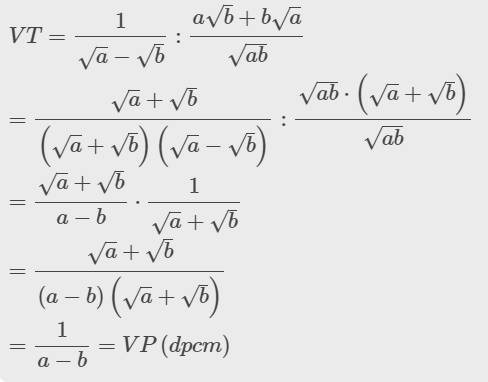Các câu hỏi tương tự
Bài: Cho M=\(\dfrac{\sqrt{a}+\sqrt{b}-1}{a+\sqrt{ab}}\) + \(\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\) . ( \(\dfrac{b}{a-\sqrt{ab}}\) + \(\dfrac{\sqrt{b}}{a+\sqrt{ab}}\) )
a) Tìm đk của a và b để M xác định
b) C/m M > 0
cho biểu thức M=\(\dfrac{a\sqrt{a}-b\sqrt{b}}{a-b}-\dfrac{a}{\sqrt{a}+\sqrt{b}}-\dfrac{b}{\sqrt{b}-\sqrt{a}}\) với a,b>0 và a khác b
Rút gọn M và tính giá trị biểu thức M biết (1-a).(1-b)+\(2\sqrt{ab}=1\)
Chứng minh các đẳng thức sau:
c) \(\dfrac{\sqrt{a}+\sqrt{b}}{2\sqrt{a}-2\sqrt{b}}-\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{a}+2\sqrt{b}}-\dfrac{2b}{b-a}=\dfrac{2\sqrt{b}}{\sqrt{a}-\sqrt{b}}\) ( với a,b > 0 và a \(\ne\) b )
Bài 1: Tính
a) \(\sqrt{1,44.1,21-1,44.0,4}\)
b) \(\dfrac{\sqrt{5}-2}{\sqrt{5}+2}+\sqrt{80}\)
c) \(\sqrt[3]{16}+\sqrt[3]{2}\left(\sqrt[3]{4}-\sqrt[3]{2}\right)\)
Bài 2: C/m
\(\dfrac{1}{\sqrt{a}-\sqrt{b}}:\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}=\dfrac{1}{a-b}\) với a,b>0, a khác 0
1. chứng minh rằng các hằng đẳng thức sau với điều kiện các biểu thức tồn tại:
a) \(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}:\dfrac{1}{\sqrt{a}-\sqrt{b}}=a-b\)
b)\(\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)=1-a\)
cho M= \(\dfrac{\sqrt{a}+\sqrt{b}-1}{a+a\sqrt{b}}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\left(\dfrac{\sqrt{b}}{a\sqrt{ab}}+\dfrac{\sqrt{b}}{a+\sqrt{ab}}\right)\)
a) tìm điều kiện a và b để M xác định
b) c/m M>0
Bài 3:
Rút gọn: \(\dfrac{a\sqrt{b}+b}{a-b}\sqrt{\dfrac{ab+b^2-2\sqrt{ab^3}}{a\left(a+2\sqrt{b}\right)+b}}:\dfrac{1}{\sqrt{a}+\sqrt{b}}\) với a > 0, b \(\ge\) 0
Cần gấp !!!
Chứng minh đẳng thức:
a) \(\dfrac{\sqrt{a}}{\sqrt{a}-\sqrt{b}}-\dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}}-\dfrac{2b}{a-b}=\dfrac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
( với a > hoặc bằng 0; b > hoặc bằng 0; a khác b )
với a > 0, b > 0 thì \(\sqrt{\dfrac{a}{b}}+\dfrac{a}{b}\sqrt{\dfrac{b}{a}}\)bằng:
a) 2
b) \(\dfrac{2\sqrt{ab}}{b}\)
c) \(\sqrt{\dfrac{a}{b}}\)
d) \(\sqrt{\dfrac{2a}{b}}\)