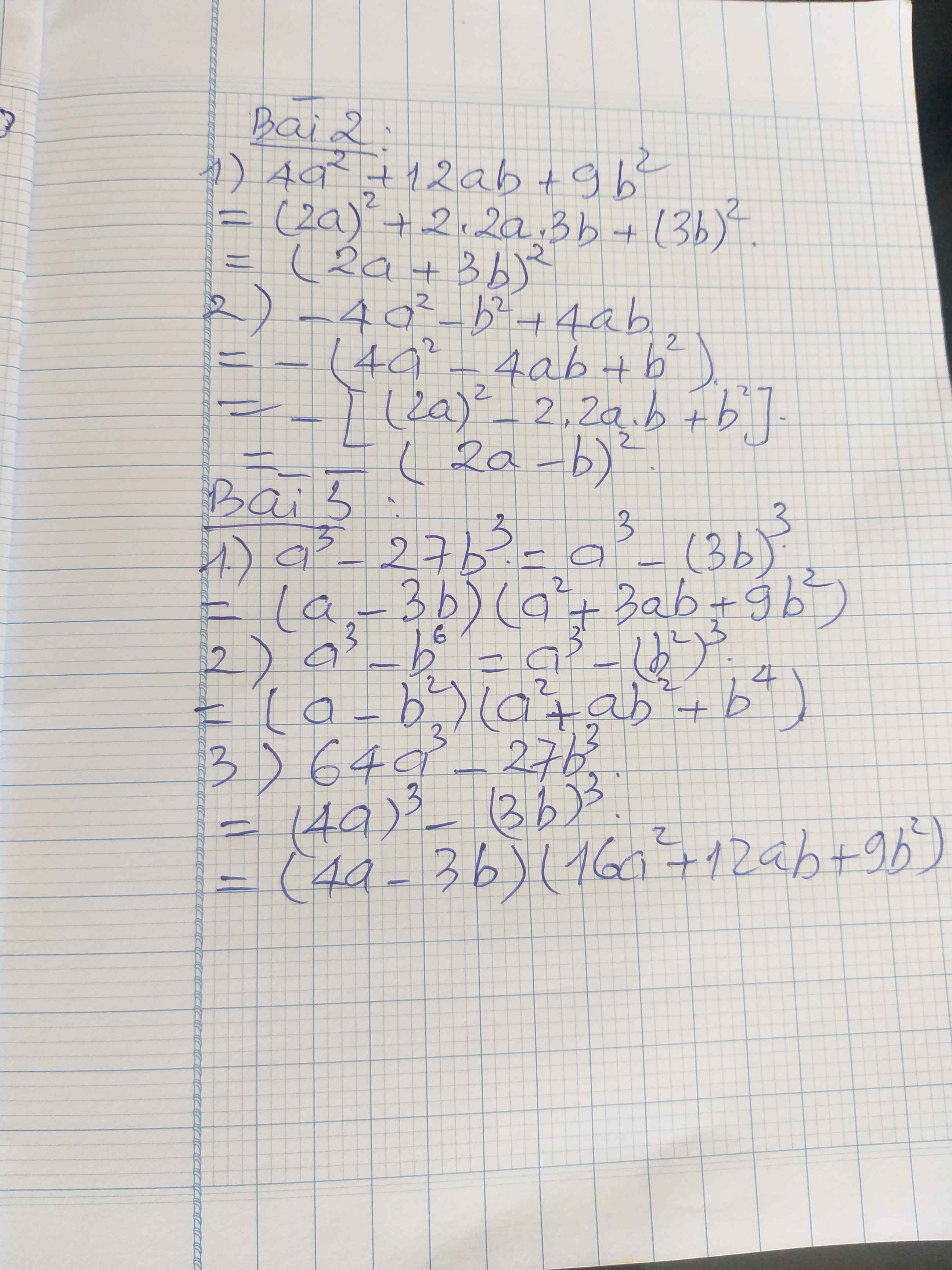Bài 1: Phân tích các đa thứa sau thành nhân tử:
A) ( a - 3) 2 4
B) ( a - 2b)2 - b2
C) (4a + 3b)2 - ( 2a + b)2
D) ( 2a - b)2 - ( a - b )2
E) ( x - y )2 - ( 2x - y )2
Bài 2: Phân tích các đa thức thành nhân tử:
1) 4a2 + 12ab + 9b2
2) -4a2 - b2 + 4ab
Bài 3: phân tích các đa thức thành nhân tử|
1)a3 - 27b3
2) a3 - b6
3) 64a3 - 27b3
Bài 1:
`a)(a-3)^2-4`
`=(a-3)^2-2^2`
`=(a-3-2)(a-3+2)`
`=(a-5)(a-1)`
`b)(a-2b)^2-b^2`
`=(a-2b-b)(a-2b+b)`
`=(a-3b)(a-b)`
`c)(4a+3b)^2-(2a+b)^2`
`=(4a+3b+2a+b)(4a+3b-2a-b)`
`=(6a+4b)(2a+2b)`
`d)(2a-b)^2-(a-b)^2`
`=(2a-b-a+b)(2a-b+a-b)`
`=a(3a-2b)`
`e)(x-y)^2-(2x-y)^2`
`=(x-y-2x+y)(x-y+2x-y)`
`=-x(3x-2y)`
Bài 1:
A) \((a - 3)^2 - 4\)
\[
(a - 3)^2 - 4 = [(a - 3) - 2][(a - 3) + 2]
\]
\[
= (a - 5)(a - 1)
\]
B) \((a - 2b)^2 - b^2\)
\[
(a - 2b)^2 - b^2 = [(a - 2b) - b][(a - 2b) + b]
\]
\[
= (a - 3b)(a - b)
\]
C) \((4a + 3b)^2 - (2a + b)^2\)
\[
(4a + 3b)^2 - (2a + b)^2 = [(4a + 3b) - (2a + b)][(4a + 3b) + (2a + b)]
\]
\[
= (2a + 2b)(6a + 4b) = 2(a + b) \cdot 2(3a + 2b)
\]
\[
= 2(a + b)(3a + 2b)
\]
D) \((2a - b)^2 - (a - b)^2\)
\[
(2a - b)^2 - (a - b)^2 = [(2a - b) - (a - b)][(2a - b) + (a - b)]
\]
\[
= (a)(3a - 2b)
\]
\[
= a(3a - 2b)
\]
E) \((x - y)^2 - (2x - y)^2\)
\[
(x - y)^2 - (2x - y)^2 = [(x - y) - (2x - y)][(x - y) + (2x - y)]
\]
\[
= (-x)(3x - 2y)
\]
\[
= -x(3x - 2y)
\]
Bài 2:
1) \(4a^2 + 12ab + 9b^2\)
\[
4a^2 + 12ab + 9b^2 = (2a + 3b)^2
\]
2) \(-4a^2 - b^2 + 4ab\)
\[
-4a^2 - b^2 + 4ab = -[(2a - b)^2]
\]
\[
= -(2a - b)(2a - b)
\]
Bài 3:
1) \(a^3 - 27b^3\)
\[
a^3 - 27b^3 = (a - 3b)(a^2 + 3ab + 9b^2)
\]
2) \(a^3 - b^6\)
\[
a^3 - b^6 = (a - b^2)(a^2 + ab^2 + b^4)
\]
3) \(64a^3 - 27b^3\)
\[
64a^3 - 27b^3 = (4a - 3b)(16a^2 + 12ab + 9b^2)
\]