a) \(A=\dfrac{L}{2}=\dfrac{8}{2}=4\left(cm\right)\)
\(T=\dfrac{50}{20}=2,5\left(s\right)\)
b) \(\omega=\dfrac{2\pi}{T}=\dfrac{2.3,14}{2,5}\sim2,51\left(rad/s\right)\)
Chọn gốc thời gian là lúc vật qua vị trí \(x=-3\left(cm\right)\) theo chiều dương (hướng ra biên dương), phương trình dao động là
\(x=Acos(ωt+\varphi)=4cos\left(2,51t+\varphi\right)\)
\(t=0;x=-3\Rightarrow-3=4cos\varphi\Rightarrow\varphi=2,42\left(rad\right)\)
\(\Rightarrow x=4cos(2,51t+2,42)\left(cm\right)\)
\(\Rightarrow v=-4.2,51sin(2,51t+2,42)=-10,04sin(2,51t+2,42)\left(cm/s\right)\)
\(\Rightarrow a=-4.\left(2,51\right)^2cos(2,51t+2,42)=-25,2cos(2,51t+2,42)\left(cm/s^2\right)\)
a, Vật dao động điều hòa với quỹ đạo dài 8cm ⇒ 2A = 8 ⇒ A = 4 (cm)
Trong 50s, vật thực hiện được 20 dao động \(\Rightarrow f=\dfrac{20}{50}=\dfrac{2}{5}\left(Hz\right)\)
Ta co': \(T=\dfrac{1}{f}=\dfrac{1}{\dfrac{2}{5}}=\dfrac{5}{2}=2,5\left(s\right)\)
Vậy biên độ dao động là 4cm, chu kì 2,5 s
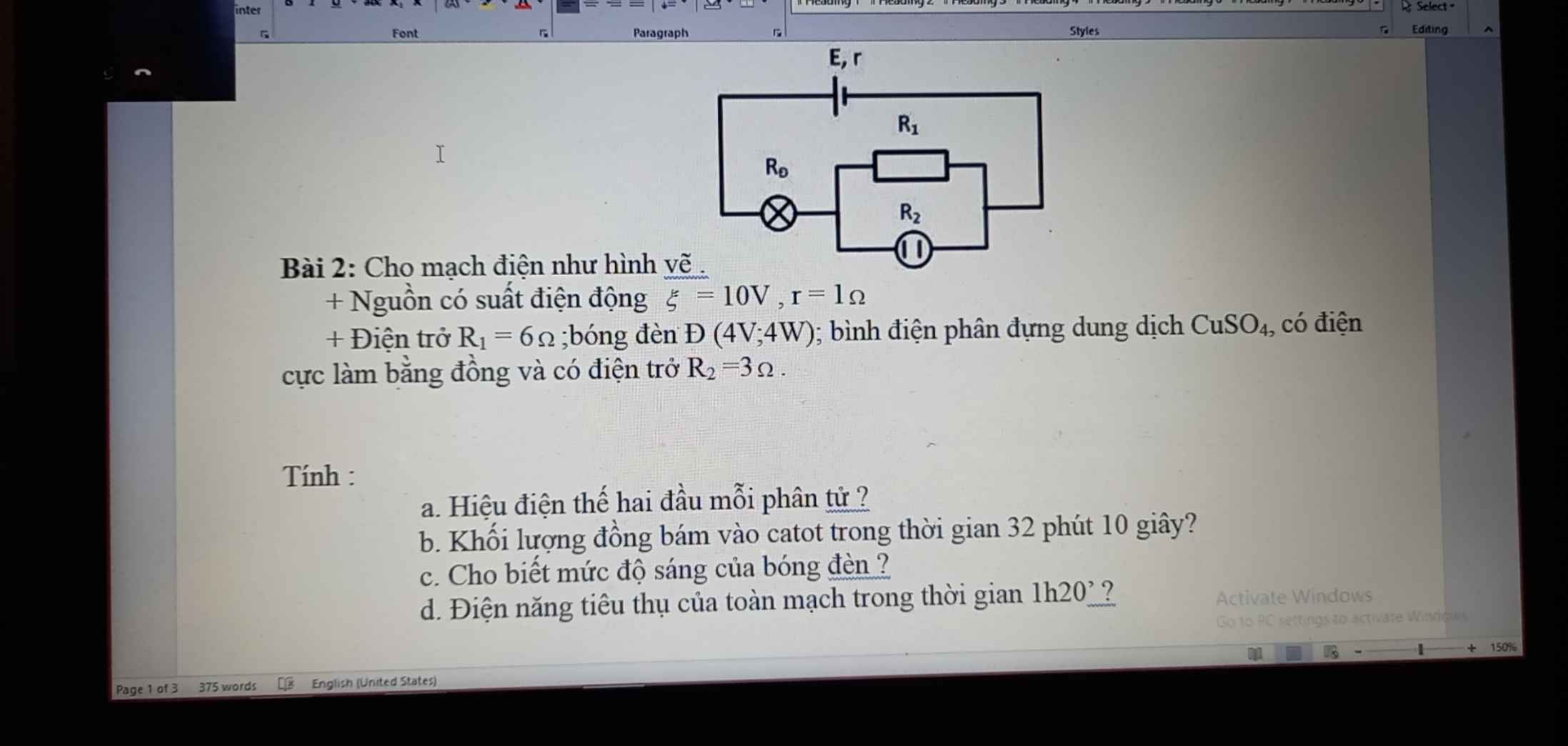giúp em bài này với ạ 
