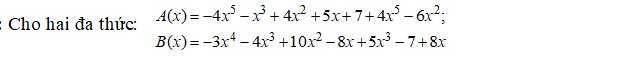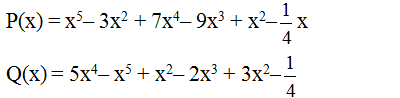Ủa em, sao \(P\left(x\right)=A\left(x\right)+B\left(x\right)\) rồi lại \(P\left(x\right)=A\left(x\right)-B\left(x\right)\) nữa
Phải là \(Q\left(x\right)=A\left(x\right)-B\left(x\right)\) chứ ko đến câu c làm sao biết P(x) là cái nào trong 2 cái của câu b?
`#3107.101107`
`a)`
`A(x) = -4x^5 - x^3 + 4x^2 + 5x + 7 + 4x^5 - 6x^2`
`= (-4x^5 + 4x^5) - x^3 + (4x^2 - 6x^2) + 5x + 7`
`= -x^3 - 2x^2 + 5x + 7`
`B(x) = -3x^4 - 4x^3 + 10x^2 - 8x + 5x^3 - 7 + 8x`
`= -3x^4 - (4x^3 - 5x^3) + 10x^2 - (8x - 8x) - 7`
`= -3x^4 - x^3 + 10x^2 - 7`
`b)`
`P(x) = A(x) + B(x)`
`=> P(x)(1) = -x^3 - 2x^2 + 5x + 7 + -3x^4 - x^3 + 10x^2 - 7`
`= -3x^4 + (-x^3 - x^3) - (2x^2 - 10x^2) + 5x + (7 - 7)`
`= -3x^4 - 2x^3 + 8x^2 + 5x`
`P(x)(2) = A(x) - B(x)`
`=> P(x) = -x^3 - 2x^2 + 5x + 7 - (-3x^4 - x^3 + 10x^2 - 7)`
`= -x^3 - 2x^2 + 5x + 7 + 3x^4 + x^3 - 10x^2 + 7`
`= 3x^4 + (x^3 - x^3) - (2x^2 + 10x^2) + 5x + (7 + 7)`
`= 3x^4 - 12x^2 + 5x + 14`
`c)`
Thay `x = -1` vào đa thức `P(x)(2):`
`3*(-1)^4 - 12*(-1)^2 + 5*(-1) + 14`
`= 3 * 1 - 12 * 1 - 5 + 14 = 3 - 12 - 5 + 14 = 0 `
Vậy, `x = -1` là nghiệm của đa thức `P(x)(2).`