a: E đối xứng B qua AH
=>AH là trung trực của BE
=>AH\(\perp\)BE tại trung điểm của BE
Ta có: AH\(\perp\)BE
AH\(\perp\)BC
BE,BC có điểm chung là B
Do đó: B,E,C thẳng hàng
=>AH\(\perp\)BC tại trung điểm của BE
=>H là trung điểm của BE
D đối xứng A qua BC
=>BC là đường trung trực của AD
=>BC\(\perp\)AD tại trung điểm của aD
Ta có: BC\(\perp\)AD
BC\(\perp\)AH
AD,AH có điểm chung là A
Do đó: A,H,D thẳng hàng
=>BC\(\perp\)AH tại trung điểm của AD
=>H là trung điểm của AD
Xét tứ giác ABDE có
H là trung điểm chung của AD và BE
=>ABDE là hình bình hành
Hình bình hành ABDE có AD\(\perp\)BE tại H
nên ABDE là hình thoi
b: Gọi O là trung điểm của CE
Xét (O) có
ΔCKE nội tiếp
CE là đường kính
Do đó: ΔCKE vuông tại K
=>CK\(\perp\)KE tại E
=>EK\(\perp\)AC tại K
Ta có: EK\(\perp\)AC
AB\(\perp\)AC
Do đó: EK//AB
mà ED//AB(ABDE là hình thoi)
và EK,ED có điểm chung là E
nên E,D,K thẳng hàng

 a, b thôi ạ!
a, b thôi ạ!







 A,B vs vẽ hình thôi ạ
A,B vs vẽ hình thôi ạ
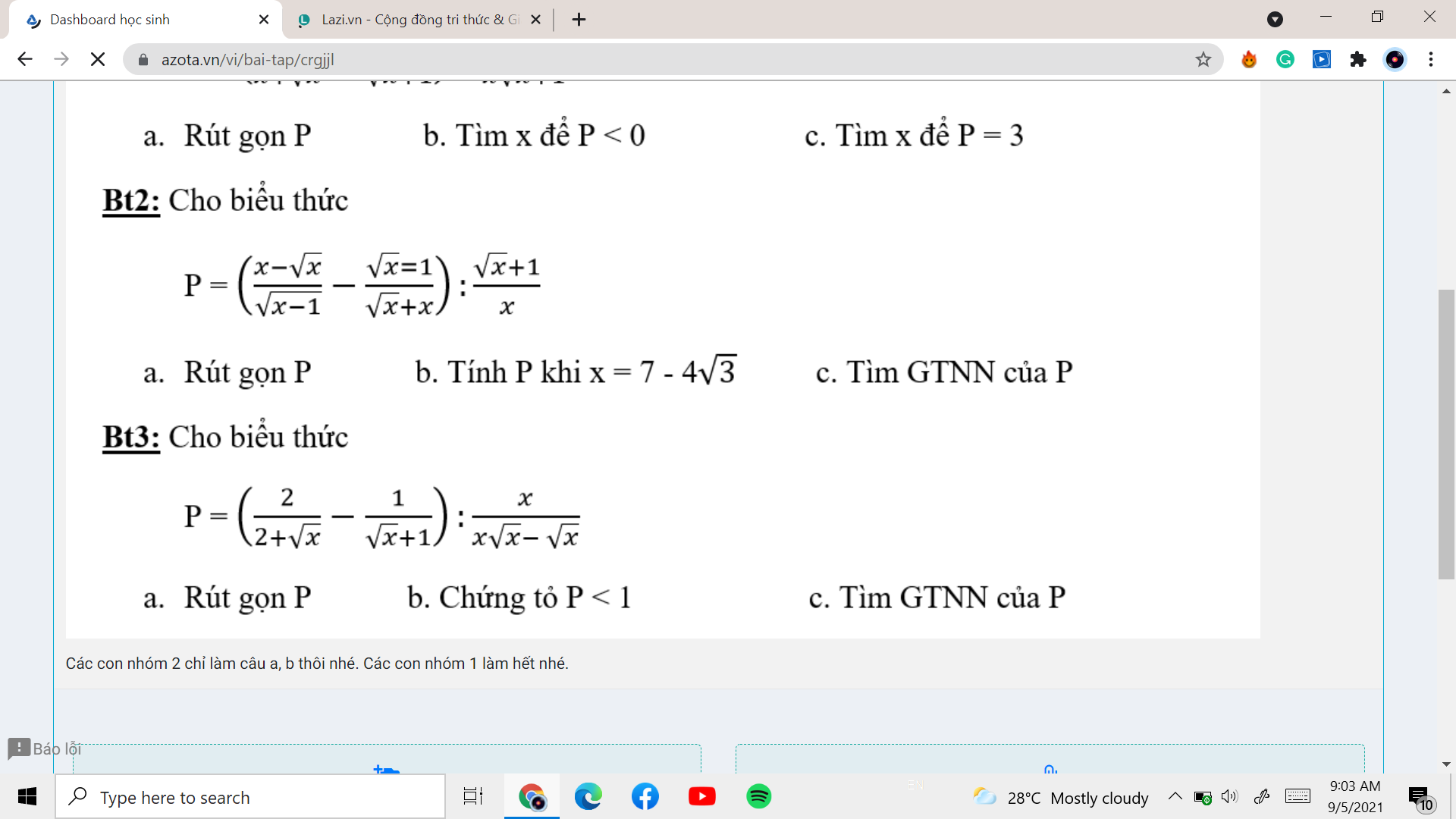


 vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á
vẽ hình vs làm câu a) . b) thôi ạ, e cần gấp lắm á




