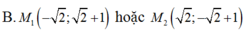Để AM nhỏ nhất thì AM=d(A;(d))
=>\(AM=\dfrac{\left|2\cdot1+0\cdot\left(-4\right)+15\right|}{\sqrt{1^2+\left(-4\right)^2}}=\dfrac{17}{\sqrt{17}}=\sqrt{17}\)
Gọi (d1): ax+by+c=0 là phương trình đường thẳng đi qua A và vuông góc với (d)
(d): x-4y+15=0; A(2;0)
Vì (d1)\(\perp\)(d)
nên (d1): 4x+y+c=0
Thay x=2 và y=0 vào (d1), ta được:
\(c+4\cdot2+0=0\)
=>c=-8
=>(d1): 4x+y-8=0
Tọa độ M là:
\(\left\{{}\begin{matrix}4x+y-8=0\\x-4y+15=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+y=8\\x-4y=-15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}16x+4y=32\\x-4y=-15\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}17x=17\\4x+y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=4\end{matrix}\right.\)
vậy: M(1;4)