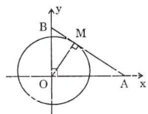
Gọi tiếp điểm của AB và đường tròn tâm O, bán kính 1 là M, ta có: OM ⊥ AB.
ΔOAB vuông tại O, có OM là đường cao nên MA.MB = MO2 = 1 (hằng số)
Áp dụng bất đẳng thức Cô-si ta có:
MA + MB ≥ 2√MA.MB = 2. √1 = 2
Dấu « = » xảy ra khi MA = MB = 1.
Khi đó OA = √(MA2 + MO2) = √2 ; OB = √(OM2 + MB2) = √2.
Mà A, B nằm trên tia Ox và Oy nên A(√2; 0); B(0; √2)
Vậy tọa độ là A(√2, 0) và B(0, √2).