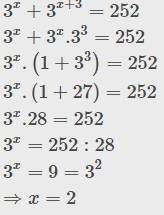3x + 3x+3 = 252
3x.28=252
3x=252:28
3x=9
3x=32
=>x=2
\(3^x+3^{x+3}=252\)
\(3^x+3^x.3^3=252\)
\(3^x.\left(1+3^3\right)=252\)
\(3^x.\left(1+27\right)=252\)
\(3^x.28=252\)
\(3^x=252:28\)
\(3^x=9=3^2\)
\(\Rightarrow x=2\)
\(3^x+3^{x+3}=252\\\Rightarrow 3^x+3^x\cdot3^3=252\\\Rightarrow3^x\cdot(1+3^3)=252\\\Rightarrow3^x\cdot(1+27)=252\\\Rightarrow3^x\cdot28=252\\\Rightarrow3^x=252:28\\\Rightarrow3^x=9\\\Rightarrow3^x=3^2\\\Rightarrow x=2\\Vậy:x=2\)
Bạn chỉnh lại phần lớp học nhé!
\(3^x+3^{x+3}=252\\ \Leftrightarrow3^x+27.3^x=252\\ \Leftrightarrow\left(1+27\right).3^x=252\\ \Leftrightarrow28.3^x=252\\ \Leftrightarrow3^x=9\\ \Leftrightarrow3^x=3^2\\ \Rightarrow x=2\)
Vậy x = 2
3^x+3^(x+3)=252
<=>3^x+3^x.3^3=252
<=>3^x.(1+27)=252
<=>3^x=9
<=>x=3
Vậy x=3
