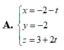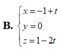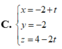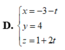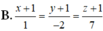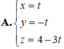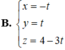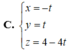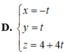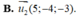1)Giao điểm của d: \(\dfrac{x+1}{2}=\dfrac{y-4}{-2}=\dfrac{z+2}{1}\) và mặt phẳng (P): x+2y-z-6=0 là
2)Điểm đối xứng với điểm M (4;2;1) qua mặt phẳng (P): 4x+y+2z+1=0 là
3)Hình chiếu của điểm M(1;1;-1) lên đường thẳng d: \(\dfrac{x-4}{2}=\dfrac{y-4}{2}=\dfrac{z-2}{-1}\) là
4)Điểm đối xứng với điểm M (2;0;1) qua đường thẳng d: \(\dfrac{x+1}{1}=\dfrac{y+4}{2}=\dfrac{z}{1}\) là
5)Cho mặt phẳng (P): 2x+y+z-3=0 và đường thẳng d : \(\dfrac{x-1}{2}=\dfrac{y-2}{-1}=\dfrac{z-3}{1}\).Hình chiếu của (d) trên (P) có phương trình là
6)Cho mặt phẳng (P):x-z-4=0 và đường thẳng d: \(\dfrac{x-3}{3}=\dfrac{y-1}{1}=\dfrac{z+1}{-1}\).Hình chiếu của d trên (P) có phương trình là
1.
Phương trình d dạng tham số: \(\left\{{}\begin{matrix}x=-1+2t\\y=4-2t\\z=-2+t\end{matrix}\right.\) (1)
Giao điểm (d) và (P) thỏa mãn:
\(-1+2t+2\left(4-2t\right)-\left(-2+t\right)-6=0\)
\(\Rightarrow t=1\)
Thay vào (1) ta được tọa độ giao điểm: \(\left(1;2;-1\right)\)
2.
Gọi (d) là đường thẳng qua M và vuông góc (P)
\(\Rightarrow\) (d) nhận (4;1;2) là 1 vtcp
Phương trình (d): \(\left\{{}\begin{matrix}x=4+4t\\y=2+t\\z=1+2t\end{matrix}\right.\)
Gọi A là giao điểm của (d) và (P), tọa độ A thỏa mãn:
\(4\left(4+4t\right)+2+t+2\left(1+2t\right)+1=0\)
\(\Rightarrow t=-1\Rightarrow A\left(0;1;-1\right)\)
M' đối xứng M qua (P) \(\Rightarrow A\) là trung điểm MM'
\(\Rightarrow M'\left(-4;0;-3\right)\)
3.
Gọi (P) là mặt phẳng qua M và vuông góc (d)
\(\Rightarrow\) d nhận (2;2;-1) là 1 vtpt
Phương trình (P):
\(2\left(x-1\right)+2\left(y-1\right)-\left(z+1\right)=0\)
\(\Leftrightarrow2x+2y-z-5=0\)
Phương trình (d) dạng tham số: \(\left\{{}\begin{matrix}x=4+2t\\y=4+2t\\z=2-t\end{matrix}\right.\)
Gọi H là hình chiếu của M lên (d)
\(\Rightarrow\) H là giao điểm (P) và (d)
Tọa độ H thỏa mãn:
\(2\left(4+2t\right)+2\left(4+2t\right)-\left(2-t\right)-5=0\)
\(\Rightarrow t=-1\)
\(\Rightarrow H\left(2;2;3\right)\)
4.
Gọi (P) là mp qua M và vuông góc (d)
\(\Rightarrow\) (P) nhận (1;2;1) là 1 vtpt
Phương trình (P):
\(1\left(x-2\right)+2\left(y-0\right)+1\left(z-1\right)=0\)
\(\Leftrightarrow x+2y+z-3=0\)
Phương trình (d) dạng tham số: \(\left\{{}\begin{matrix}x=-1+t\\y=-4+2t\\z=t\\\end{matrix}\right.\)
GỌi H là hình chiếu vuông góc của M lên (d)
\(\Rightarrow\) H là giao điểm (d) và (P)
Tọa độ H thỏa mãn:
\(-1+t+2\left(-4+2t\right)+t-3=0\)
\(\Rightarrow t=2\Rightarrow H\left(1;0;2\right)\)
M' đối xứng M qua (d) \(\Rightarrow H\) là trung điểm MM'
\(\Rightarrow M'\left(0;0;3\right)\)
5.
Phương trình (d) dạng tham số: \(\left\{{}\begin{matrix}x=1+2t\\y=2-t\\z=3+t\end{matrix}\right.\)
Gọi M là giao điểm (d) và (P), tọa độ M thỏa mãn:
\(2\left(1+2t\right)+2-t+3+t-3=0\)
\(\Rightarrow t=-1\)
\(\Rightarrow M\left(-1;3;2\right)\)
Lấy \(A\left(1;2;3\right)\) thuộc (d), gọi (d') là đường thẳng qua A và vuông góc (P)
\(\Rightarrow\left(d'\right)\) nhận (2;1;1) là 1 vtcp
Phương trình (d'): \(\left\{{}\begin{matrix}x=1+2t'\\y=2+t'\\z=3+t'\end{matrix}\right.\)
Gọi N là giao điểm của (d') và (P), tọa độ N thỏa:
\(2\left(1+2t'\right)+2+t'+3+t'-3=0\)
\(\Rightarrow t'=-\dfrac{2}{3}\Rightarrow N\left(-\dfrac{1}{3};\dfrac{4}{3};\dfrac{7}{3}\right)\)
\(\Rightarrow\overrightarrow{NM}=\left(\dfrac{4}{3};\dfrac{5}{3};-\dfrac{1}{3}\right)=\dfrac{1}{3}\left(4;5;-1\right)\)
Đường thẳng MN chính là hình chiếu của (d) lên (P)
Phương trình MN: \(\dfrac{x+1}{4}=\dfrac{y-3}{5}=\dfrac{z-2}{-1}\)
Câu 6 cách làm giống hệt câu 5 ko khác gì cả. (giao điểm \(M\left(3;1;-1\right)\) và lấy \(O\left(0;0;0\right)\) thuộc (d) để tìm hình chiếu lên (P)