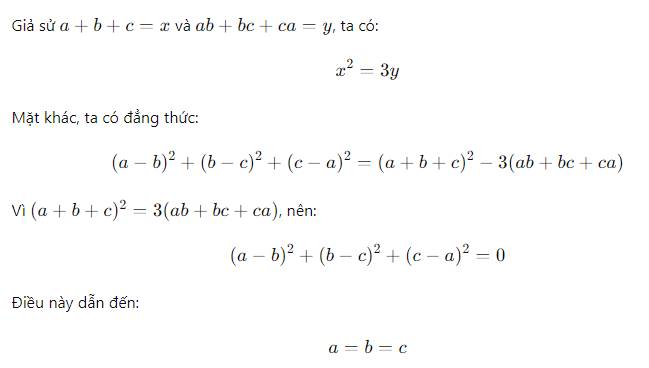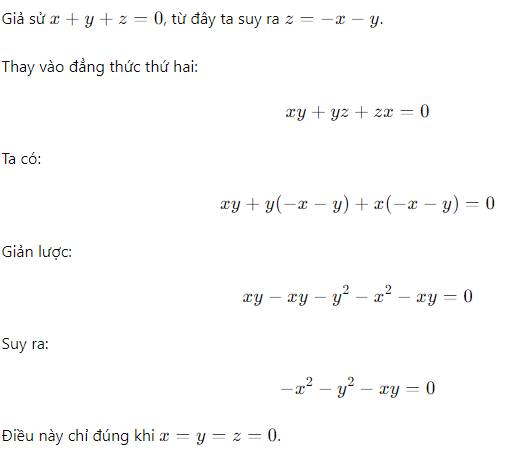1) \(\left(a+b+c\right)^2=3\left(ab+ac+bc\right)\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac=3\left(ab+bc+ac\right)\)
\(\Leftrightarrow a^2+b^2+c^2=\left(3ab+3ac+3bc\right)-\left(2ab+2bc+2ac\right)\)
\(\Leftrightarrow a^2+b^2+c^2=ab+ac+bc\)
\(\Leftrightarrow2\left(a^2+b^2+c^2\right)=2ab+2ac+2bc\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-2ac+c^2\right)+\left(b^2-2bc+c^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b=0\\a-c=0\\b-c=0\end{matrix}\right.\Leftrightarrow a=b=c\)
2) Ta có: \(x+y+z=0\Leftrightarrow\left(x+y+z\right)^2=0\)
\(\Leftrightarrow x^2+y^2+z^2+2xy+2xz+2yz=0\)
\(\Leftrightarrow x^2+y^2+z^2+2\left(xy+xz+yz\right)=0\)
\(\Leftrightarrow x^2+y^2+z^2+2\cdot0=0\)
\(\Leftrightarrow x^2+y^2+z^2=0\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0\\z=0\end{matrix}\right.\Leftrightarrow x=y=z=0\)
3) \(A=1^2-2^2+3^2-4^2+...+2003^2-2004^2+2005^2\)
\(A=\left(2005^2-2004^2\right)+\left(2003^2-2002^2\right)+...+\left(3^2-2^2\right)+1^2\)
\(A=\left(2005+2004\right)\left(2005-2004\right)+\left(2003-2002\right)\left(2003+2002\right)+...+\left(3-2\right)\left(3+2\right)+1^2\)
\(A=4009+4005+...+5+1^2\)
\(A=\left(5+9+...+4005+4009\right)+1\)
\(A=\dfrac{\left(4009+5\right)\cdot\left[\left(4009-5\right):4+1\right]}{2}+1\)
\(A=\dfrac{4014\cdot1002}{2}+1\)
\(A=2011015\)