Các câu hỏi tương tự
1.88 Cho DABC đều, gọi O là trung điểm của cạnh BC,xOy60 độ có cạnh Ox, Oy luôn cắt AB, AC tại M và N. Chứng minh :a) DOB M sim DNOC suy ra OB2 BM . CNb) DOBM sim ∼DONM suy ra MO, NO lần lượt là tia phân giác và .BM . CN dfrac{1}{4} BC2.
Đọc tiếp
1.88 Cho DABC đều, gọi O là trung điểm của cạnh BC,xOy=60 độ có cạnh Ox, Oy luôn cắt AB, AC tại M và N. Chứng minh :
a) DOB M \(\sim\) DNOC suy ra OB2 = BM . CN
b) DOBM \(\sim\) ∼
DONM suy ra MO, NO lần lượt là tia phân giác và .
BM . CN =\(\dfrac{1}{4}\) BC2.
cho tam giác ABC đều O là trung điểm của BC, góc xOy=60 độ có cạnh Ox, Oy luôn cắt AB, AC tại M và N.
a)cmr OB^2=BM*CN
b)cmr tia MO, NO luôn là phân giác của góc BMN và CMN
c) cmr đường thẳng MN luôn tiếp xúc với một đường tròn cố định khi góc xOy quay quanh o nhưng hai cạnh Ox, Oy vẫn cắt hai cạnh AB và AC của tam giác ABC
mn giúp mình câu c với ạ!
Cho tam giác ABC đều với O là trung điểm của cạnh BC. Một góc xOy=60 độ có cạnh Ox cắt AB tại M,Oy căt AC tại N. Chứng minh:
a, BC2=4BM.CN
b, MO và NO lần lượt là phân giác của các góc BMN và MNC
c, đường thẳng MN luôn cách O một khoảng không đổi khi goc xOy xoay quanh O sao cho Ox, Oy vẫn cắt cạnh AB, AC của tam giác ABC
14 tháng 1 2022 lúc 20:40
Cho tam giác ABC đều có cạnh bằng a. Gọi O là trung điểm của BC. Một góc xOy bằng 60o quay quanh điểm O sao cho hai cạnh Ox, Oy luôn cắt AB và AC lần lượt tại M và N.a) cm: Tam giác OBM đồng dạng với tam giác NCO.b) cm: BC24BM.CN.c) Khoảng cách từ điểm O đến MN không đổi khi Ox; Oy thay đổi.d) Từ O vẽ đường thẳng d bất kì cắt AB; AC tại P; Q.CMR: dfrac{1}{AP}+dfrac{1}{AQ} không đổi.
Đọc tiếp
Cho tam giác ABC đều có cạnh bằng a. Gọi O là trung điểm của BC. Một góc xOy bằng 60o quay quanh điểm O sao cho hai cạnh Ox, Oy luôn cắt AB và AC lần lượt tại M và N.
a) cm: Tam giác OBM đồng dạng với tam giác NCO.
b) cm: BC2=4BM.CN.
c) Khoảng cách từ điểm O đến MN không đổi khi Ox; Oy thay đổi.
d) Từ O vẽ đường thẳng d bất kì cắt AB; AC tại P; Q.
CMR: \(\dfrac{1}{AP}+\dfrac{1}{AQ}\) không đổi.
CHo tam giác cân ABC , O là trung điểm của BC.Trên AB,AC lần lượt lấy các điểm di động M và N sao cho góc MON = 60 độ.C/m rằng:
a) Tam giác OMB đồng dạng với tam giác NOC tứ đó suy ra BM nhân CN ko đổi.
b) Các tia MO , NO lần lượt là các tia phân giác của góc BMN , góc CNM.
c)chu vi tam giác amn ko đổi
Cho tam giác ABC vuông tại A (AB AC) ngoại tiếp đường tròn tâm O. Gọi D,E,F lần lượt là tiếp điểm của (O) với các cạnh AB,AC,BC. Đường thẳng BO cắt các đường thẳng EF và DF lần lượt tại I và K.2. Giả sử M là điểm di chuyển trên đoạn CE .a. Khi AM AB, gọi H là giao điểm của BM và EF. Chứng minh rằng ba điểm A,O,H thẳng hàng, từ đó suy ra tứ giác ABHI nội tiếp.b. Gọi N là giao điểm của đường thẳng BM với cung nhỏ EF của (O), P, Q lần lượt là hình chiếu của N trên các đường thẳng DE...
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC) ngoại tiếp đường tròn tâm O. Gọi D,E,F lần lượt là tiếp điểm của (O) với các cạnh AB,AC,BC. Đường thẳng BO cắt các đường thẳng EF và DF lần lượt tại I và K.
2. Giả sử M là điểm di chuyển trên đoạn CE .
a. Khi AM = AB, gọi H là giao điểm của BM và EF. Chứng minh rằng ba điểm A,O,H thẳng hàng, từ đó suy ra tứ giác ABHI nội tiếp.
b. Gọi N là giao điểm của đường thẳng BM với cung nhỏ EF của (O), P, Q lần lượt là hình chiếu của N trên các đường thẳng DE và DF. Xác định vị trí điểm M để độ dài đoạn thẳng PQ max.
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE 60o.a) Chứng minh tích BD.CE không đổi.b) Chứng minh ΔBOD ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Đọc tiếp
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE = 60o.
a) Chứng minh tích BD.CE không đổi.
b) Chứng minh ΔBOD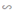 
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE
60
o
.a) Chứng minh tích BD.CE không đổi.b) Chứng minh ΔBOD ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Đọc tiếp
Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE = 60 o .
a) Chứng minh tích BD.CE không đổi.
b) Chứng minh ΔBOD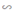 
ΔOED. Từ đó suy ra tia DO là tia phân giác của góc BDE.
c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.
Cho tam giác ABC có 3 góc nhọn (AB<AC). Vẽ đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại N, M. Gọi H là giao điểm của BM vfa CN; AH cắt BC tại K.
a) Chứng minh tứ giác ANKC nội tiếp
b) Gọi I là giao điểm của NK và BM. Chứng minh: IH.NM=IN.MH
c) Chứng minh tứ giác NKOM nội tiếp