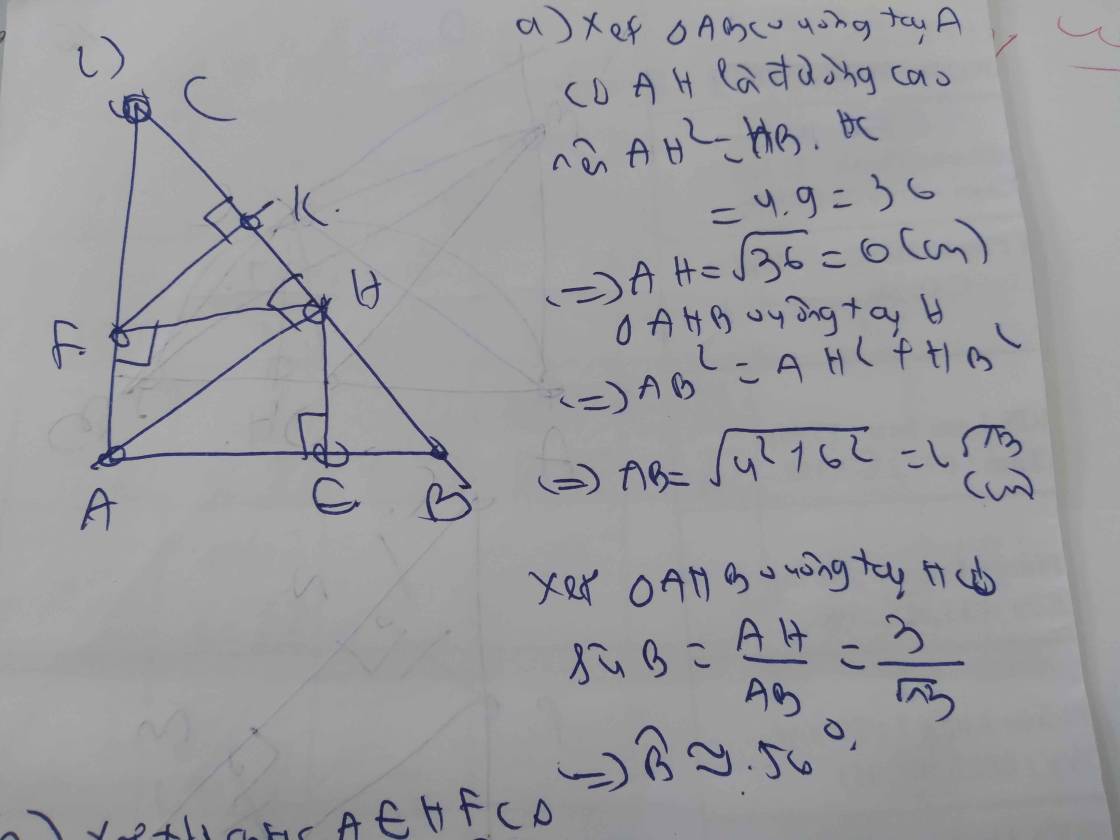
1) Tính chiều cao của một cột đèn (làm tròn đến mét), biết bóng của của cột đèn được chiếu bởi ánh sáng mặt trời xuống đất dài và góc tạo bởi tia sáng với mặt đất là (hình vẽ dưới).
2) Cho ▲ ABC vuông tại A, đường cao AH .
a) Giả sử HB=4 cm và HC=9 cm. Tính AB,AH , và số đo ABC (số đo góc làm tròn đến độ).
b) Gọi E là hình chiếu của H trên AB , F là hình chiếu của H trên AC .
Chứng minh AH=EF và chứng minh \(AE.AB+AF.AC=2EF^2\) .
c) Vẽ FK vuông góc vs BC (K ϵ BC). Chứng minh \(KF=\dfrac{HC}{tanAHF+cotACB}\) .
Bài 2
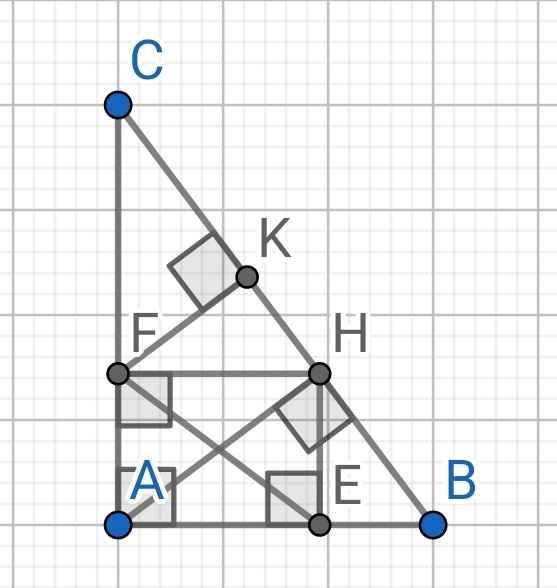a) ∆ABC vuông tại A, AH là đường cao
⇒ AH² = BH.HC
= 4.9
= 36
⇒ AH = 6 (cm)
BC = BH + HC
= 4 + 9 = 13 (cm)
∆ABC vuông tại A, AH là đường cao
⇒ AB² = BH.BC
= 4.13
= 52 (cm)
⇒ AB = 2√13 (cm)
⇒ cos ABC = AB/BC
= 2√13/13
⇒ ∠ABC ≈ 56⁰
b) ∆AHB vuông tại H, HE là đường cao
⇒ AH² = AE.AB (1)
∆AHC vuông tại H, HF là đường cao
⇒ AH² = AF.AC (2)
Từ (1) và (2) suy ra:
AE.AB + AF.AC = 2AH² (3)
Xét tứ giác AEHF có:
∠HFA = ∠FAE = ∠AEH = 90⁰ (gt)
⇒ AEHF là hình chữ nhật
⇒ AH = EF (4)
Từ (3) và (4) suy ra:
AE.AB + AF.AC = 2EF²
Bài 1
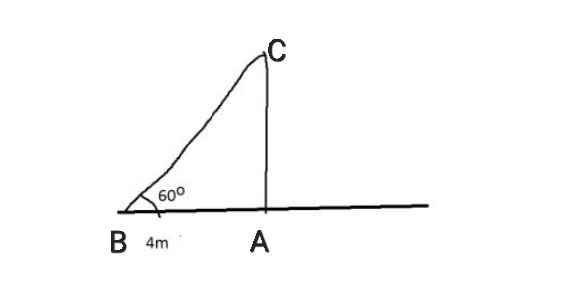Ta có:
tan B = AC/AB
⇒ AC = AB . tan B
= 4 . tan60⁰
= 4√3 (m)
≈ 7 (m)
