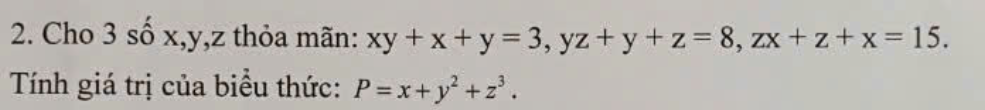\(\left\{{}\begin{matrix}xy+x+y=3\\yz+y+z=8\\zx+z+x=15\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}xy+x+y=3\left(1\right)\\y=\dfrac{8-z}{z+1}\\x=\dfrac{15-z}{z+1}\end{matrix}\right.\)
\(\left(1\right)\Rightarrow\dfrac{\left(8-z\right)\left(15-z\right)}{\left(z+1\right)^2}+\dfrac{15-z}{z+1}+\dfrac{8-z}{z+1}=3\left(ĐK:z\ne-1\right)\)
\(\Leftrightarrow\left(8-z\right)\left(15-z\right)+\left(15-z\right)\left(z+1\right)+\left(8-z\right)\left(z+1\right)=3\left(z+1\right)^2\)
\(\Leftrightarrow120-8z-15z+z^2+15z+15-z^2-z+8z+8-z^2-z=3z^2+6z+3\)
\(\Leftrightarrow-4z^2-8z+140=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}z=5\left(n\right)\\z=-7\left(n\right)\end{matrix}\right.\)
* \(z=5\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}\\y=\dfrac{1}{2}\end{matrix}\right.\)\(\Rightarrow P=x+y^2+z^3=....\)
*\(z=-7\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{11}{3}\\y=-\dfrac{5}{2}\end{matrix}\right.\)\(\Rightarrow P=...\)