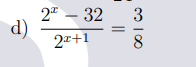Question

Answer 1

`(2^x - 32)/(2^(x + 1)) = 3/8`
`2^x - 32 = 3/8 . 2^(x + 1)`
`2^x - 32 = (3 . 2^(x + 1))/8`
`2^x - 32 = (6 . 2^x)/8`
`2^x - 32 = (3 . 2^x)/4`
`4(2^x - 32) = 3 . 2^x`
`4 . 2^x - 128 = 3 . 2^x`
`4 . 2^x - 3 . 2^x  = 128`
`2^x = 128`
`2^x = 2^7`
`x = 7`

Answer 2

\(\dfrac{2^x-32}{2^{x+1}}=\dfrac{3}{8}\)

\(\Leftrightarrow8\left(2^x-32\right)=3\cdot2^{x+1}\)

\(\Leftrightarrow8\cdot2^x-256=3\cdot2^x\cdot2\)

\(\Leftrightarrow8\cdot2^x-6\cdot2^x=256\)

\(\Leftrightarrow2\cdot2^x=256\)

\(\Leftrightarrow2^x=128\)

\(\Leftrightarrow x=7\)