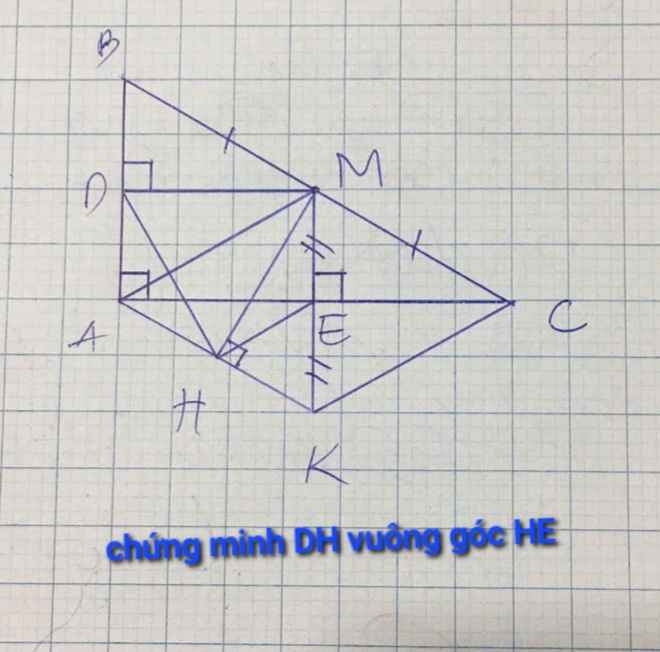
Gọi O là giao điểm của AM và DE
Xét tứ giác ADME có \(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
nên ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
=>O là trung điểm chung của AM và DE
ADME là hình chữ nhật
=>AM=DE
mà \(AO=OM=\dfrac{AM}{2};DO=OE=\dfrac{DE}{2}\)
nên \(AO=OM=DO=OE=\dfrac{AM}{2}=\dfrac{DE}{2}\)
ΔMHA vuông tại H
mà HO là đường trung tuyến
nên \(HO=\dfrac{MA}{2}=\dfrac{DE}{2}\)
Xét ΔHDE có
HO là đường trung tuyến
\(HO=\dfrac{DE}{2}\)
Do đó: ΔHDE vuông tại H
=>HD\(\perp\)HE