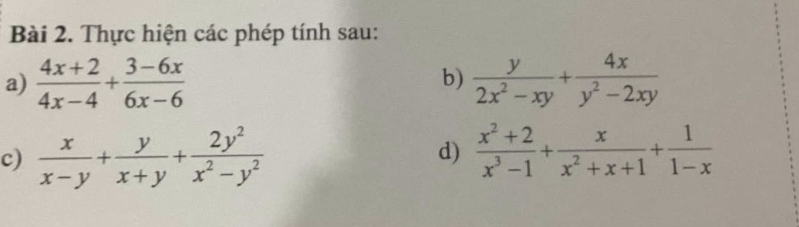a: ĐKXĐ: x<>1
\(\dfrac{4x+2}{4x-4}+\dfrac{3-6x}{6x-6}\)
\(=\dfrac{2\left(2x+1\right)}{2\left(2x-2\right)}+\dfrac{3\left(1-2x\right)}{3\left(2x-2\right)}\)
\(=\dfrac{2x+1}{2x-2}+\dfrac{1-2x}{2x-2}=\dfrac{2x+1+1-2x}{2x-2}=\dfrac{2}{2x-2}=\dfrac{1}{x-1}\)
b: \(\dfrac{y}{2x^2-xy}+\dfrac{4x}{y^2-2xy}\)
\(=\dfrac{y}{x\left(2x-y\right)}+\dfrac{4x}{y\left(y-2x\right)}\)
\(=\dfrac{y^2-4x^2}{xy\left(2x-y\right)}=\dfrac{-\left(2x-y\right)\left(2x+y\right)}{xy\left(2x-y\right)}=\dfrac{-\left(2x+y\right)}{xy}\)
c: ĐKXĐ: \(x\ne\pm y\)
\(\dfrac{x}{x-y}+\dfrac{y}{x+y}+\dfrac{2y^2}{x^2-y^2}\)
\(=\dfrac{x\left(x+y\right)+y\left(x-y\right)+2y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{x^2+xy+xy-y^2+2y^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{x^2+2xy+y^2}{\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{\left(x+y\right)^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{x+y}{x-y}\)
d: ĐKXĐ: x<>1
\(\dfrac{x^2+2}{x^3-1}+\dfrac{x}{x^2+x+1}+\dfrac{1}{1-x}\)
\(=\dfrac{x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x}{x^2+x+1}-\dfrac{1}{x-1}\)
\(=\dfrac{x^2+2+x\left(x-1\right)-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{-x+1+x^2-x}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2-2x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x-1}{x^2+x+1}\)