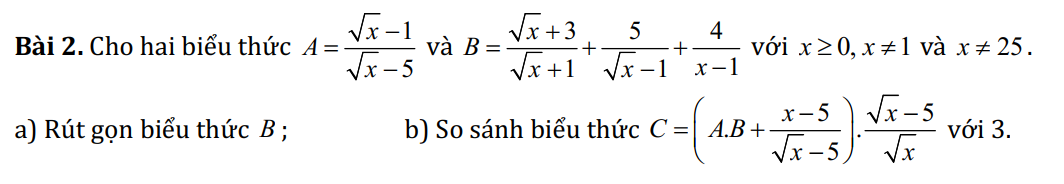a: \(B=\dfrac{\sqrt{x}+3}{\sqrt{x}+1}+\dfrac{5}{\sqrt{x}-1}+\dfrac{4}{x-1}\)
\(=\dfrac{\sqrt{x}+3}{\sqrt{x}+1}+\dfrac{5}{\sqrt{x}-1}+\dfrac{4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)+5\left(\sqrt{x}+1\right)+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+2\sqrt{x}-3+5\sqrt{x}+5+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x+7\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+6}{\sqrt{x}-1}\)
b:
ĐKXĐ: x>0; x<>1; x<>25
\(C=\left(A\cdot B+\dfrac{x-5}{\sqrt{x}-5}\right)\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}-1}{\sqrt{x}-5}\cdot\dfrac{\sqrt{x}+6}{\sqrt{x}-1}+\dfrac{x-5}{\sqrt{x}-5}\right)\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}+6}{\sqrt{x}-5}+\dfrac{x-5}{\sqrt{x}-5}\right)\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(C-3=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-3=\dfrac{x-2\sqrt{x}+1}{\sqrt{x}}=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}}>0\) với mọi x thỏa mãn ĐKXĐ
=>C>3