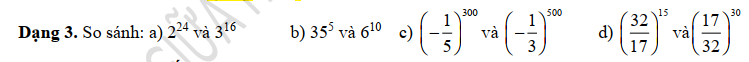\(a,\) Ta có: \(2^{24}=\left(2^3\right)^8=8^8\)
\(3^{16}=\left(3^2\right)^8=9^8\)
Vì \(8< 9\) nên \(8^8< 9^8\)
hay \(2^{24}< 3^{16}\)
\(b,\) Ta có: \(6^{10}=\left(6^2\right)^5=36^5\)
Vì \(36>35\) nên \(36^5>35^5\)
hay \(6^{10}>35^5\)
a: \(2^{24}=\left(2^3\right)^8=8^8\)
\(3^{16}=\left(3^2\right)^8=9^8\)
mà 8<9
nên \(2^{24}< 3^{16}\)
b: \(6^{10}=\left(6^2\right)^5=36^5>35^5\)
c: \(\left(-\dfrac{1}{5}\right)^{300}=\left(\dfrac{1}{5}\right)^{300}=\left(\dfrac{1}{5^3}\right)^{100}=\left(\dfrac{1}{125}\right)^{100}\)
\(\left(-\dfrac{1}{3}\right)^{500}=\left(\dfrac{1}{3}\right)^{500}=\dfrac{1}{3^{500}}=\left(\dfrac{1}{3^5}\right)^{100}=\left(\dfrac{1}{243}\right)^{100}\)
125<243
=>\(1>\dfrac{1}{125}>\dfrac{1}{243}\)
=>\(\left(\dfrac{1}{125}\right)^{100}< \left(\dfrac{1}{243}\right)^{100}\)
d: \(\left(\dfrac{17}{32}\right)^{30}=\left[\left(\dfrac{17}{32}\right)^2\right]^{15}=\left(\dfrac{289}{1024}\right)^{15}\)
Vì \(\dfrac{32}{17}>1>\dfrac{289}{1024}\)
nên \(\left(\dfrac{32}{17}\right)^{15}>\left(\dfrac{289}{1024}\right)^{15}\)
=>\(\left(\dfrac{32}{17}\right)^{15}>\left(\dfrac{17}{32}\right)^{30}\)