3
a.
ĐKXĐ: \(x\ne\left\{0;1;2;3;4;5\right\}\)
b.
\(P=\dfrac{1}{x\left(x-1\right)}+\dfrac{1}{\left(x-1\right)\left(x-2\right)}+\dfrac{1}{\left(x-2\right)\left(x-3\right)}+\dfrac{1}{\left(x-3\right)\left(x-4\right)}+\dfrac{1}{\left(x-4\right)\left(x-5\right)}\)
\(=\dfrac{1}{x-1}-\dfrac{1}{x}+\dfrac{1}{x-2}-\dfrac{1}{x-1}+\dfrac{1}{x-3}-\dfrac{1}{x-2}+\dfrac{1}{x-4}-\dfrac{1}{x-3}+\dfrac{1}{x-5}-\dfrac{1}{x-4}\)
\(=\dfrac{1}{x-5}-\dfrac{1}{x}\)
\(=\dfrac{5}{x\left(x-5\right)}\)
4.
a.
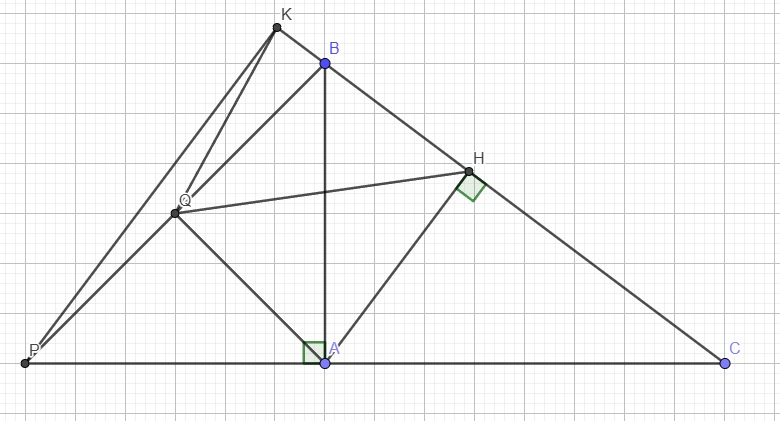
Do \(AH\perp BC\), mà \(KP||AH\) (gt)
\(\Rightarrow KP\perp BC\Rightarrow\widehat{CKP}=90^0\)
Xét hai tam giác ABC và tam giác KPC có:
\(\left\{{}\begin{matrix}\widehat{CAB}=\widehat{CKP}=90^0\\\widehat{C}\text{ là góc chung}\end{matrix}\right.\)
\(\Rightarrow\Delta ABC\sim\Delta KPC\left(g.g\right)\)
b.
Do \(KP\perp BC\left(cmt\right)\Rightarrow\Delta KBP\) vuông tại K
Mà Q là trung điểm BP \(\Rightarrow QK=\dfrac{1}{2}BP\) (trung tuyến ứng với cạnh huyền) (1)
\(\widehat{BAP}=180^0-\widehat{BAC}=90^0\Rightarrow\Delta BAP\) vuông tại A
Mà Q là trung điểm BP \(\Rightarrow QA=\dfrac{1}{2}BP\) (trung tuyến ứng với cạnh huyền) (2)
(1);(2) \(\Rightarrow QK=QA\) (3)
Theo giả thiết \(HK=HA\) (4)
(3);(4) \(\Rightarrow QH\) là trung trực của AK