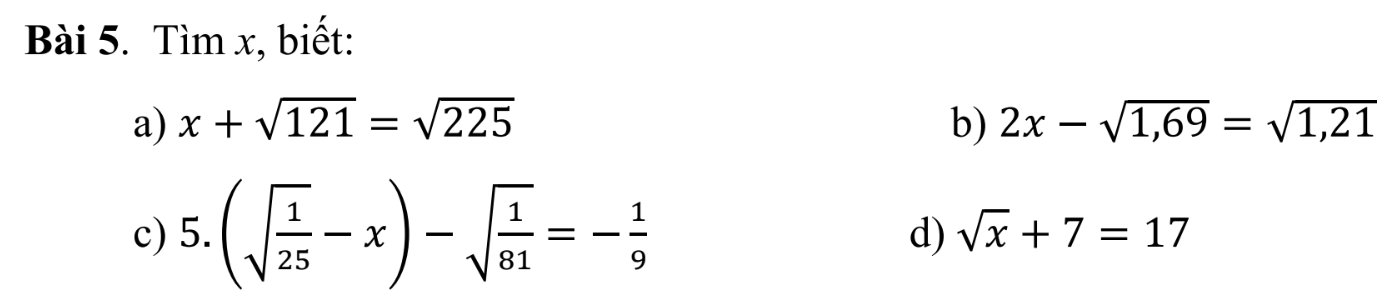a) \(x+\sqrt{121}=\sqrt{225}\)
\(x+11=15\)
\(x=15-11\)
\(x=4\)
b) \(2x-\sqrt{1,69}=\sqrt{1,21}\)
\(2x-1,3=1,1\)
\(2x=1,1+1,3\)
\(2x=2,4\)
\(x=2,4:2\)
\(x=1,2\)
c) \(5.\left(\sqrt{\dfrac{1}{25}}-x\right)-\sqrt{\dfrac{1}{81}}=-\dfrac{1}{9}\)
\(5.\left(\dfrac{1}{5}-x\right)-\dfrac{1}{9}=-\dfrac{1}{9}\)
\(5.\left(\dfrac{1}{5}-x\right)=-\dfrac{1}{9}+\dfrac{1}{9}\)
\(5.\left(\dfrac{1}{5}-x\right)=0\)
\(\dfrac{1}{5}-x=0:5\)
\(\dfrac{1}{5}-x=0\)
\(x=\dfrac{1}{5}-0\)
\(x=\dfrac{1}{5}\)
d) \(\sqrt{x}+7=17\)
\(\sqrt{x}=17-7\)
\(\sqrt{x}=10\)
\(x=100\)
`a , x + \sqrt(121) = \sqrt(225)`
`=> x + 11 = 15`
`=> x = 15 - 11`
`=> x = 4`
Vậy: `x = 4`
`b, 2x - \sqrt(1,69) = \sqrt(1,21)`
`=> 2x - 1,3 = 1,1`
`=> 2x = 1,1 + 1,3`
`=> 2x = 2,4`
`=> x = 2,4 : 2`
`=> x = 1,2`
Vậy: `x = 1,2`
`c, 5 . (\sqrt(1/25)- x) - sqrt(1/81)= -1/9`
`=> 5 . (1/5 - x) - 1/9 = -1/9`
`=> 5 . (1/5 - x) = -1/9 + 1/9`
`=> 1/5 - x = 0 : 5`
`=> 1/5 -x = 0`
`=> x = 1/5 - 0`
`=> x = 1/5`
Vậy: `x=1/5`
`d, \sqrt(x) + 7 =17`
`=> \sqrt(x) = 17 - 7`
`=> \sqrt(x) = 10`
`=> x = 100`
Vậy: `x=100`