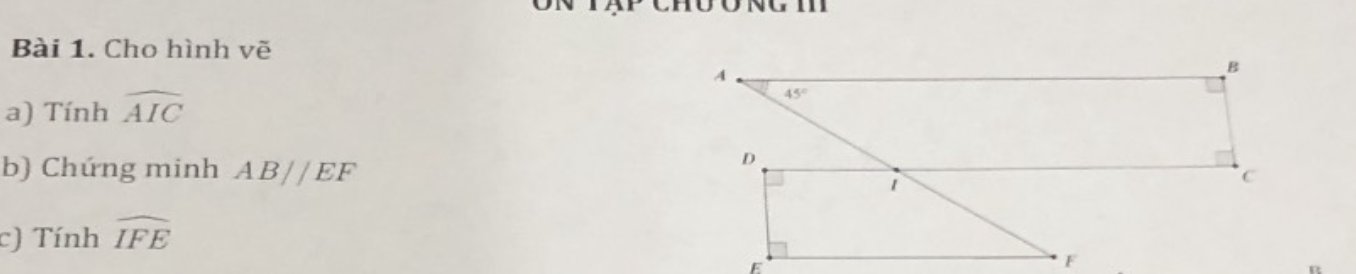
a.
Do \(\left\{{}\begin{matrix}AB\perp BC\left(gt\right)\\DC\perp BC\left(gt\right)\end{matrix}\right.\) nên \(AB||DC\) (1)
Mà \(\widehat{BAI}\) và \(\widehat{AIC}\) là hai góc trong cùng phía
Nên: \(\widehat{BAI}+\widehat{AIC}=180^0\)
\(45^0+\widehat{AIC}=180^0\)
\(\widehat{AIC}=180^0-45^0\)
\(\widehat{AIC}=135^0\)
b.
Do \(\left\{{}\begin{matrix}DC\perp DE\\EF\perp DE\end{matrix}\right.\) nên \(DC||EF\) (2)
Từ (1), (2) suy ra \(AB||EF\)
c.
Do \(AB||EF\), mà \(\widehat{IFE}\) và \(\widehat{BAI}\) là 2 góc so le trong
Nên \(\widehat{IFE}=\widehat{BAI}\)
Nên \(\widehat{IFE}=45^0\)
`a)`xét tg `ABCI` có :
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{I}=360^0\)
`=>`\(\widehat{AIC}=360^0-90^0-90^0-45^0=135^0\)
`b)` có :\(\widehat{AIC}=\widehat{DIC}=135^0\)(đối đỉnh)
Xét tg`DIFE` có :
\(\widehat{D}+\widehat{I}+\widehat{F}+\widehat{E}=360^0\)
`=>`\(\widehat{F}=45^0\)
`Lại có :\(\widehat{F}=\widehat{A}=45^0\)
Mà 2 góc ở vị trí so le trong
`=> AB` // `EF`