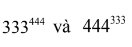Đặt 111=a
=>333=3a; 444=4a
\(333^{444}=\left(3a\right)^{4a}=\left[\left(3a\right)^4\right]^a=\left(81a^4\right)^a\)
\(444^{333}=\left(4a\right)^{3a}=\left[\left(4a\right)^3\right]^a=\left(64a^3\right)^3\)
\(81a^4-64a^3=a^3\left(81a-64\right)\)
\(=111^3\left(81\cdot111-64\right)>0\)
=>\(81a^4>64a^3\)
=>\(\left(81a^4\right)^a>\left(64a^3\right)^a\)
=>\(333^{444}>444^{333}\)
\(333^{444}\) và \(444^{333}\)
Ta có : \(333^{444}=\left(333^4\right)^{111}=\text{12296370321}^{111}\)
\(444^{333}=\left(444^3\right)^{111}=\text{87528384}^{111}\)
Vì \(\text{87528384}< \text{12296370321}\) nên \(\text{87528384}^{111}< \text{12296370321}^{111}\) hay
\(333^{444}>444^{333}\)
Vậy \(333^{444}>444^{333}\)
\(333^{444}=\left(111.3\right)^{111.4}=\left[\left(111.3\right)^4\right]^{111}=\left(111^4.3^4\right)^{111}=\left(111^4.81\right)^{111}\)
\(444^{333}=\left(111.4\right)^{3.111}=\left[\left(111.4\right)^3\right]^{111}=\left(111^3.4^3\right)^{111}=\left(111^3.64\right)^{111}\)
Do \(111^4>111^3\) và \(81>64\)
Nên \(111^4.81>111^3.64\)
Suy ra \(\left(111^4.81\right)^{111}>\left(111^3.64\right)^{111}\)
Vậy \(333^{444}>444^{333}\)