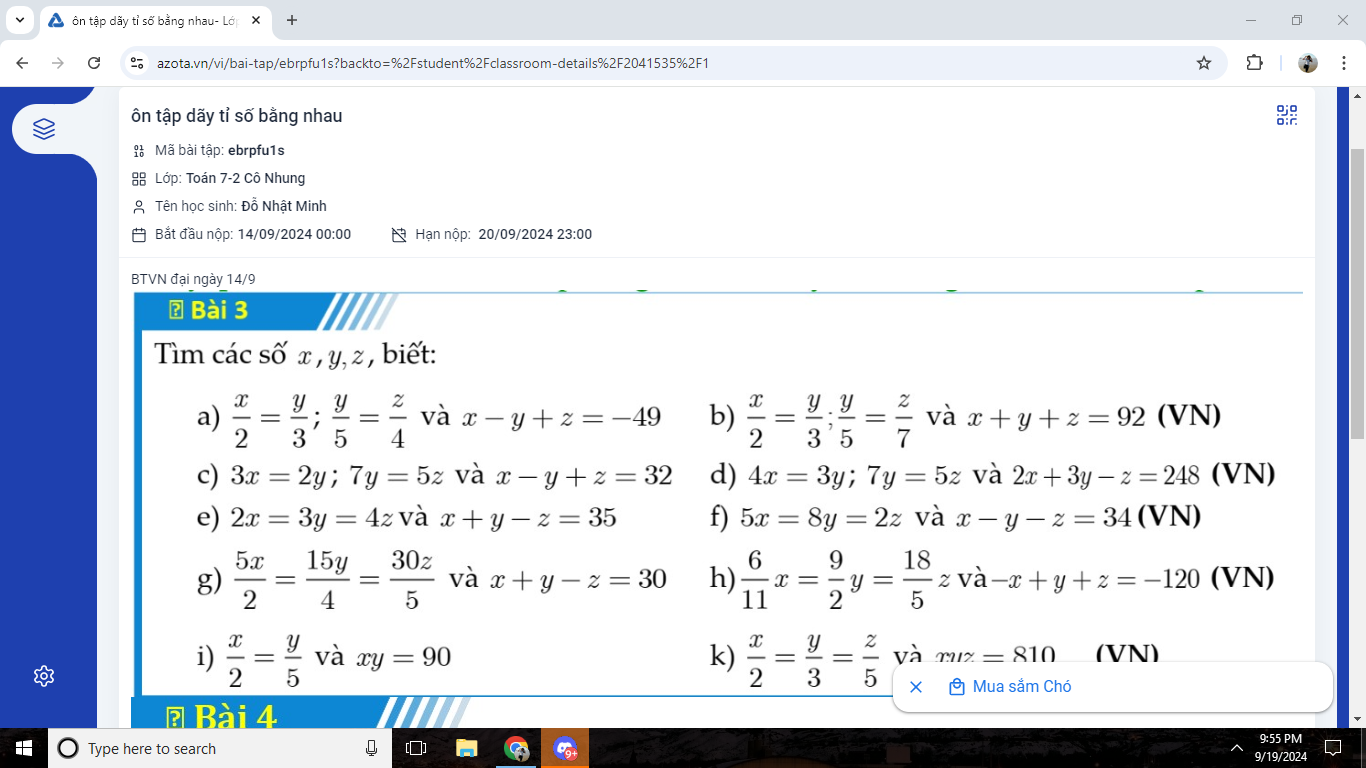
a) \(\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow y=\dfrac{3x}{2}\)
\(\dfrac{y}{5}=\dfrac{z}{4}\Rightarrow z=\dfrac{4y}{5}=\dfrac{4}{5}.\dfrac{3x}{2}=\dfrac{6x}{5}\)
\(x-y+z=-49\)
\(\Rightarrow x-\dfrac{3x}{2}+\dfrac{6x}{5}=-49\)
\(\Rightarrow\left(1-\dfrac{3}{2}+\dfrac{6}{5}\right)x=-49\)
\(\Rightarrow\dfrac{7x}{10}=-49\Rightarrow x=-\dfrac{49.10}{7}=-70\)
\(\Rightarrow y=\dfrac{3}{2}.\left(-70\right)=-105\)
\(\Rightarrow z=\dfrac{6}{5}.\left(-70\right)=-84\)
Vậy \(\left\{{}\begin{matrix}x=-70\\y=-105\\z=-84\end{matrix}\right.\)
e) \(2x=3y=4z\)
\(\Rightarrow\dfrac{2x}{12}=\dfrac{3y}{12}=\dfrac{4z}{12}\)
\(\Rightarrow\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{x+y-z}{6+4-3}=\dfrac{35}{7}=5\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{6}=5\\\dfrac{y}{4}=5\\\dfrac{z}{3}=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=30\\y=20\\z=15\end{matrix}\right.\)
a: \(\dfrac{x}{2}=\dfrac{y}{3}\)
=>\(\dfrac{x}{10}=\dfrac{y}{15}\left(7\right)\)
\(\dfrac{y}{5}=\dfrac{z}{4}\)
=>\(\dfrac{y}{15}=\dfrac{z}{12}\left(8\right)\)
Từ (7),(8) suy ra \(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{12}\)
mà x-y+z=-49
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{12}=\dfrac{x-y+z}{10-15+12}=\dfrac{-49}{7}=-7\)
=>\(x=-7\cdot10=-70;y=-7\cdot15=-105;z=-7\cdot12=-84\)
c: 3x=2y
=>\(\dfrac{x}{2}=\dfrac{y}{3}\)
=>\(\dfrac{x}{10}=\dfrac{y}{15}\left(5\right)\)
7y=5z
=>\(\dfrac{y}{5}=\dfrac{z}{7}\)
=>\(\dfrac{y}{15}=\dfrac{z}{21}\left(6\right)\)
Từ (5),(6) suy ra \(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}\)
mà x-y+z=32
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x-y+z}{10-15+21}=\dfrac{32}{16}=2\)
=>\(x=2\cdot10=20;y=2\cdot15=30;z=2\cdot21=42\)
e: 2x=3y=4z
=>\(\dfrac{2x}{12}=\dfrac{3y}{12}=\dfrac{4z}{12}\)
=>\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}\)
mà x+y-z=35
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{x+y-z}{6+4-3}=\dfrac{35}{7}=5\)
=>\(x=5\cdot6=30;y=5\cdot4=20;z=5\cdot3=15\)
g: \(\dfrac{5x}{2}=\dfrac{15y}{4}=\dfrac{30z}{5}\)
=>\(\dfrac{x}{\dfrac{2}{5}}=\dfrac{y}{\dfrac{4}{15}}=\dfrac{z}{\dfrac{5}{30}}\)
mà x+y-z=30
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{2}{5}}=\dfrac{y}{\dfrac{4}{15}}=\dfrac{z}{\dfrac{5}{30}}=\dfrac{x+y-z}{\dfrac{2}{5}+\dfrac{4}{15}-\dfrac{5}{30}}=\dfrac{30}{\dfrac{12}{30}+\dfrac{8}{15}-\dfrac{5}{30}}=30:\dfrac{15}{30}=30\cdot\dfrac{30}{15}=60\)
=>\(x=60\cdot\dfrac{2}{5}=24;y=60\cdot\dfrac{4}{15}=16;z=\dfrac{5}{30}\cdot60=10\)
i: Đặt \(\dfrac{x}{2}=\dfrac{y}{5}=k\)
=>x=2k; y=5k
xy=90
=>\(2k\cdot5k=90\)
=>\(10k^2=90\)
=>\(k^2=9\)
=>\(\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\)
TH1: k=3
\(x=2\cdot3=6;y=5\cdot3=15\)
TH2: k=-3
\(x=2\cdot\left(-3\right)=-6;y=5\cdot\left(-3\right)=-15\)
b: \(\dfrac{x}{2}=\dfrac{y}{3}\)
=>\(\dfrac{x}{10}=\dfrac{y}{15}\left(3\right)\)
\(\dfrac{y}{5}=\dfrac{z}{7}\)
=>\(\dfrac{y}{15}=\dfrac{z}{21}\left(4\right)\)
Từ (3),(4) suy ra \(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}\)
mà x+y+z=92
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
=>\(x=2\cdot10=20;y=2\cdot15=30;z=2\cdot21=42\)
d: 4x=3y
=>\(\dfrac{x}{3}=\dfrac{y}{4}\)
=>\(\dfrac{x}{15}=\dfrac{y}{20}\left(1\right)\)
7y=5z
=>\(\dfrac{y}{5}=\dfrac{z}{7}\)
=>\(\dfrac{y}{20}=\dfrac{z}{28}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
mà 2x+3y-z=248
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x+3y-z}{2\cdot15+3\cdot20-28}=\dfrac{248}{62}=4\)
=>\(x=4\cdot15=60;y=4\cdot20=80;z=4\cdot28=112\)
f: 5x=8y=2z
=>\(\dfrac{5x}{40}=\dfrac{8y}{40}=\dfrac{2z}{40}\)
=>\(\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{z}{20}\)
mà x-y-z=34
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{5}=\dfrac{z}{20}=\dfrac{x-y-z}{8-5-20}=\dfrac{34}{-17}=-2\)
=>\(x=-2\cdot8=-16;y=-2\cdot5=-10;z=-2\cdot20=-40\)
h: \(\dfrac{6}{11}x=\dfrac{9}{2}y=\dfrac{18}{5}z\)
=>\(\dfrac{x}{\dfrac{11}{6}}=\dfrac{y}{\dfrac{2}{9}}=\dfrac{z}{\dfrac{5}{18}}\)
mà -x+y+z=-120
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{11}{6}}=\dfrac{y}{\dfrac{2}{9}}=\dfrac{z}{\dfrac{5}{18}}=\dfrac{-x+y+z}{-\dfrac{11}{6}+\dfrac{2}{9}+\dfrac{5}{18}}=\dfrac{-120}{-\dfrac{4}{3}}=90\)
=>\(x=90\cdot\dfrac{11}{6}=165;y=90\cdot\dfrac{2}{9}=20;z=90\cdot\dfrac{5}{18}=25\)
k: Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}=k\)
=>x=2k; y=3k; z=5k
xyz=810
=>\(2k\cdot3k\cdot5k=810\)
=>\(30k^3=810\)
=>\(k^3=27\)
=>k=3
\(x=2\cdot3=6;y=3\cdot3=9;z=5\cdot3=15\)