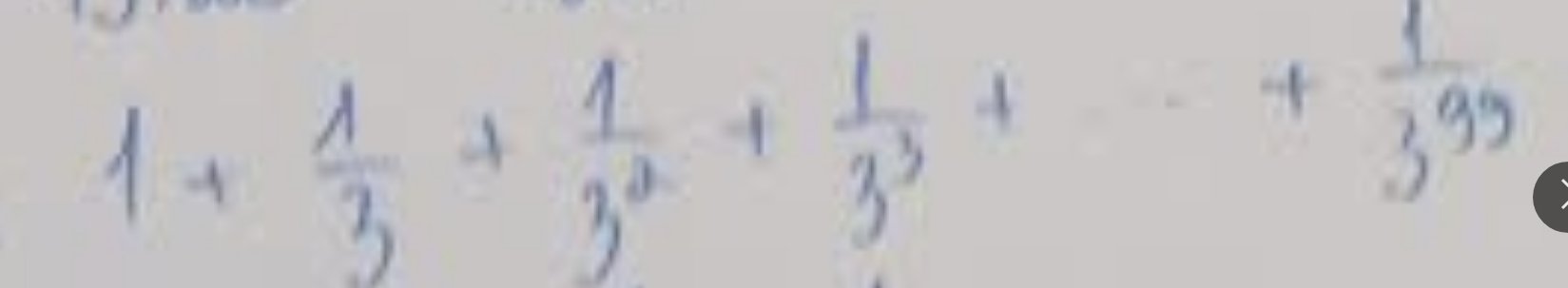Question

Answer 1

Đặt \(A=1+\dfrac{1}{3}+...+\dfrac{1}{3^{99}}\)

=>\(3A=3+1+...+\dfrac{1}{3^{98}}\)

=>\(3A-A=3+1+...+\dfrac{1}{3^{98}}-1-\dfrac{1}{3}-...-\dfrac{1}{3^{99}}\)

=>\(2A=3-\dfrac{1}{3^{99}}=\dfrac{3^{100}-1}{3^{99}}\)

=>\(A=\dfrac{3^{100}-1}{2\cdot3^{99}}\)

Answer 2

Đặt `A = 1 + 1/3 + 1/3^2 + 1/3^3 + ... + 1/3^99`

`=> 3 A = 3 + 1 + 1/3 + 1/^2 + ... + 1/3^98`

`=> 3A - A = (3 + 1 + 1/3 + 1/^2 + ... + 1/3^98) - (1 + 1/3 + 1/3^2 + 1/3^3 + ... + 1/3^99)`

`=> 2A = 3  - 1/3^99`

`=>  A = (3 - 1/3^99)/2`