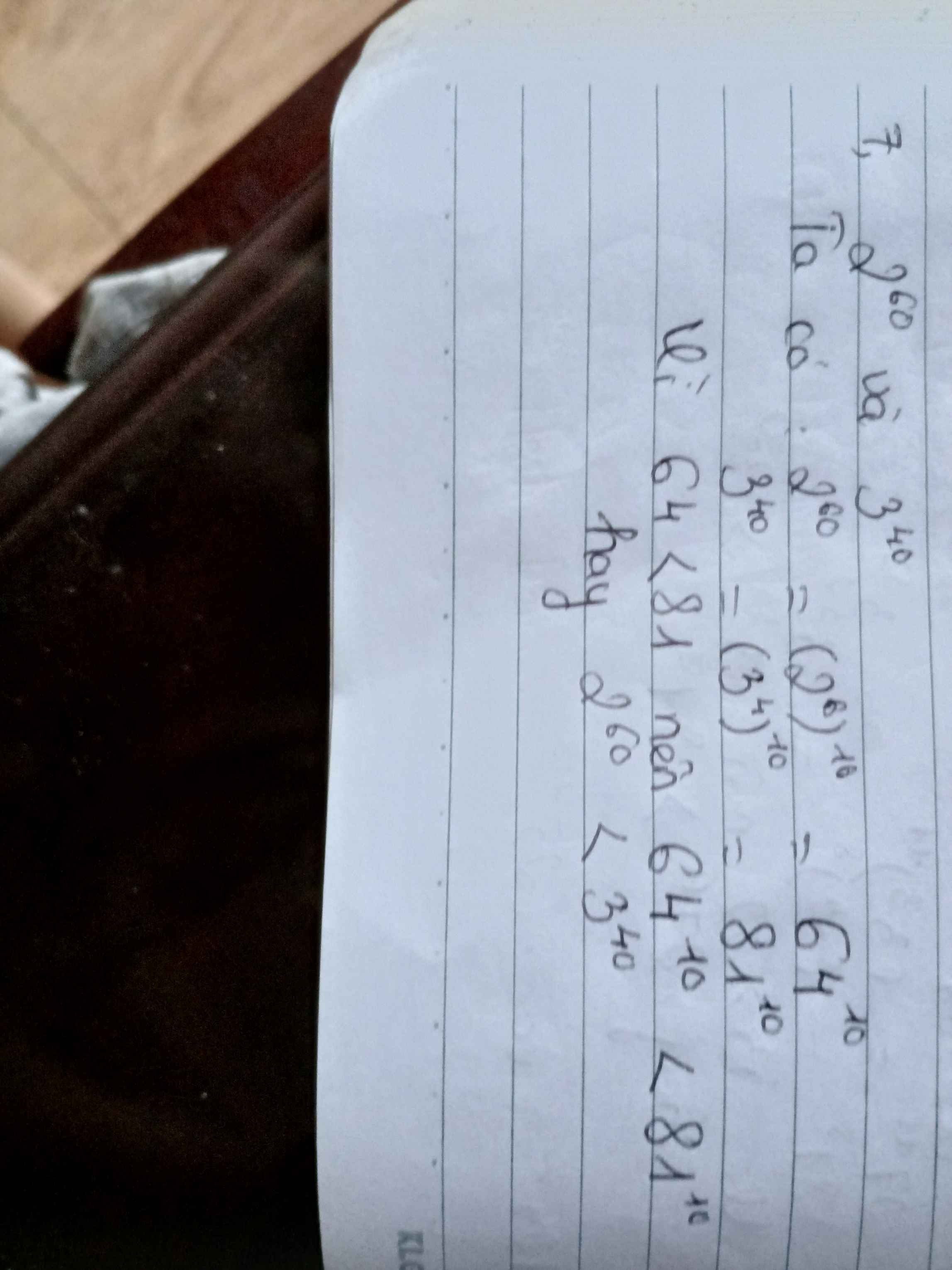\(1,\) \(9^{12}\) và \(27^7\)
Ta có: \(9^{12}=\left(3^2\right)^{12}=3^{24}\)
\(27^7=\left(3^3\right)^7=3^{21}\)
Vì \(24>21\) nên \(3^{24}>3^{21}\)
hay \(9^{12}>27^7\)
\(2,\) Ta có: \(27^{11}=\left(3^3\right)^{11}=3^{33}\)
\(81^8=\left(3^4\right)^8=3^{32}\)
Vì \(33>32\) nên \(3^{33}>3^{32}\)
hay \(27^{11}>81^8\)
3, Ta có: \(125^{80}=\left(5^3\right)^{80}=5^{240}\)
\(25^{118}=\left(5^2\right)^{118}=5^{236}\)
Vì \(240>236\) nên \(5^{240}>5^{236}\)
hay \(125^{80}>25^{118}\)
4, Ta có: \(64^8=\left(2^6\right)^8=2^{48}\)
\(16^{12}=\left(2^4\right)^{12}=2^{48}\)
Vì \(48=48\) nên \(2^{48}=2^{48}\)
hay \(64^8=16^{12}\)
5, Ta có: \(25^{15}=\left(5^2\right)^{15}=5^{30}\)
Vì \(45>30\) nên \(5^{45}>5^{30}\)
hay \(5^{45}>25^{15}\)
6, Ta có: \(625^5=\left(5^4\right)^5=5^{20}\)
\(125^7=\left(5^3\right)^5=5^{15}\)
Vì \(20>15\) nên \(5^{20}>5^{15}\)
hay \(625^5>125^7\)
7)
\(2^{60}=\left(2^3\right)^{20}=8^{20}\)
\(3^{40}=\left(3^2\right)^{20}=9^{20}\)
Do 8 < 9 \(\Rightarrow8^{20}< 9^{20}\)
Vậy \(2^{60}< 3^{40}\)
8) \(5^{36}=\left(5^3\right)^{12}=125^{12}\)
\(11^{24}=\left(11^2\right)^{12}=121^{12}\)
Do 125 > 121 \(\Rightarrow125^{12}>121^{12}\)
Vậy \(5^{36}>11^{24}\)
9) \(2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(5^{200}=\left(5^2\right)^{100}=25^{100}\)
Do 8 < 25 \(\Rightarrow8^{100}< 25^{100}\)
Vậy \(2^{300}< 5^{200}\)