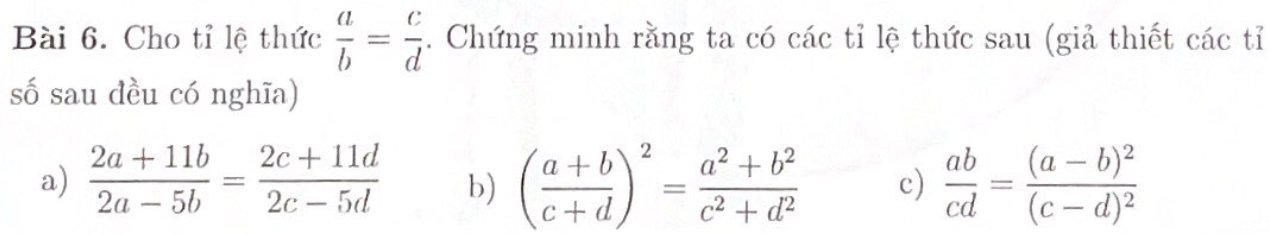Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>a=bk; c=dk
a: \(\dfrac{2a+11b}{2a-5b}=\dfrac{2\cdot bk+11b}{2\cdot bk-5b}=\dfrac{b\left(2k+11\right)}{b\left(2k-5\right)}=\dfrac{2k+11}{2k-5}\)
\(\dfrac{2c+11d}{2c-5d}=\dfrac{2\cdot dk+11d}{2\cdot dk-5d}=\dfrac{d\left(2k+11\right)}{d\left(2k-5\right)}=\dfrac{2k+11}{2k-5}\)
Do đó: \(\dfrac{2a+11b}{2a-5b}=\dfrac{2c+11d}{2c-5d}\)
b: \(\left(\dfrac{a+b}{c+d}\right)^2=\left(\dfrac{bk+b}{dk+d}\right)^2=\left[\dfrac{b\left(k+1\right)}{d\left(k+1\right)}\right]^2=\left(\dfrac{b}{d}\right)^2\)
\(\dfrac{a^2+b^2}{c^2+d^2}=\dfrac{b^2k^2+b^2}{d^2k^2+d^2}=\dfrac{b^2\left(k^2+1\right)}{d^2\left(k^2+1\right)}=\dfrac{b^2}{d^2}\)
Do đó: \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)
c: \(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2}{d^2}\)
\(\left(\dfrac{a-b}{c-d}\right)^2=\left(\dfrac{bk-b}{dk-d}\right)^2=\left[\dfrac{b\left(k-1\right)}{d\left(k-1\right)}\right]^2=\left(\dfrac{b}{d}\right)^2\)
Do đó: \(\dfrac{ab}{cd}=\left(\dfrac{a-b}{c-d}\right)^2\)