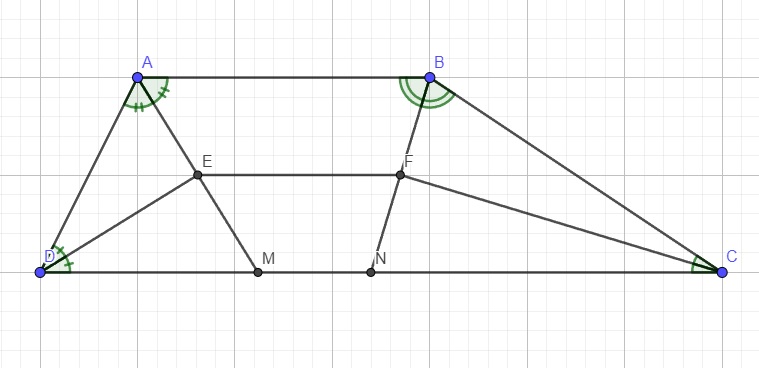
Gọi giao điểm của AE, BF với CD lần lượt tại M và N
Ta có: \(\left\{{}\begin{matrix}\widehat{DAE}=\dfrac{1}{2}\widehat{DAB}\\\widehat{ADE}=\dfrac{1}{2}\widehat{ADC}\end{matrix}\right.\) (phân giác)
\(\Rightarrow\widehat{DAE}+\widehat{ADE}=\dfrac{1}{2}\left(\widehat{DAB}+\widehat{ADC}\right)\)
Mà \(\widehat{DAB}+\widehat{ADC}=180^0\) (t/c hình thang)
\(\Rightarrow\widehat{DAE}+\widehat{ADE}=90^0\)
\(\Rightarrow\widehat{DEA}=180^0-\left(\widehat{DAE}+\widehat{ADE}\right)=90^0\)
\(\Rightarrow DE\perp AE\) hay \(DE\perp AM\)
\(\Rightarrow\) Trong tam giác ADM, DE vừa là đường cao vừa là phân giác
\(\Rightarrow\Delta ADM\) cân tại D
\(\Rightarrow DE\) đồng thời là trung tuyến
\(\Rightarrow E\) là trung điểm AM
Chứng minh tương tự ta có \(\Delta BCN\) cân tại C \(\Rightarrow CF\) đồng thời là trung tuyến
\(\Rightarrow F\) là trung điểm BM
\(\Rightarrow EF\) là đường trung bình hình thang ABNM
\(\Rightarrow EF||AB\)