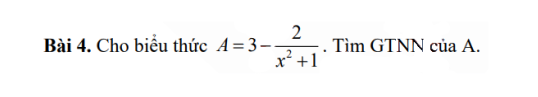Question

Answer 1

\(x^2+1>=1\forall x\)

=>\(\dfrac{2}{x^2+1}< =\dfrac{2}{1}=2\forall x\)

=>\(-\dfrac{2}{x^2+1}>=-2\forall x\)

=>\(A=-\dfrac{2}{x^2+1}+3>=-2+3=1\forall x\)

Dấu '=' xảy ra khi x=0

Answer 2

Ta có:

\(x^2\ge0\forall x\)

\(\Rightarrow x^2+1\ge1\)

\(\Rightarrow\dfrac{2}{x^2+1}\le2\)

\(\Rightarrow-\dfrac{2}{x^2+1}\ge-2\)

\(\Rightarrow3-\dfrac{2}{x^2+1}\ge3-2=1\)

\(\Rightarrow A\ge1\)

Dấu "=" xảy ra khi \(x=0\)

Vậy \(A_{min}=1\) khi \(x=0\)