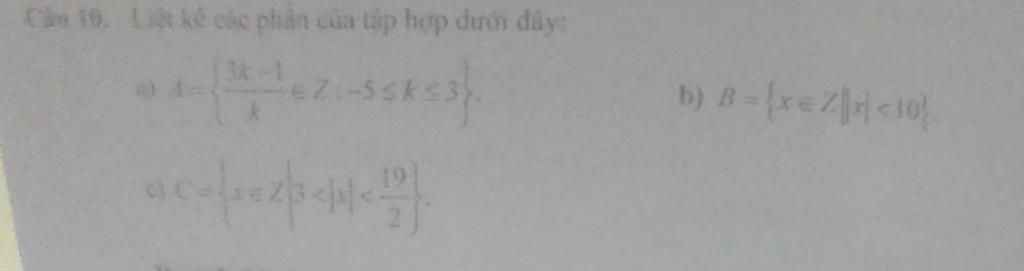Question

Answer 1

a: Để \(\dfrac{3k-1}{k}\in Z\) thì \(3k-1⋮k\)

=>\(-1⋮k\)

=>\(k\in\left\{1;-1\right\}\)

Vậy: A={1;-1}

b: |x|<10

mà x nguyên

nên \(\left|x\right|\in\left\{0;1;2;...;9\right\}\)

=>\(x\in\left\{0;1;-1;2;-2;...;9;-9\right\}\)

Vậy: B={0;1;-1;2;-2;...;9;-9}

c: 3<|x|<19/2

=>3<|x|<9,5

mà x nguyên

nên \(\left|x\right|\in\left\{4;5;6;7;8;9\right\}\)

=>\(x\in\left\{4;-4;5;-5;6;-6;7;-7;8;-8;9;-9\right\}\)

vậy: A={4;-4;5;-5;6;-6;7;-7;8;-8;9;-9}