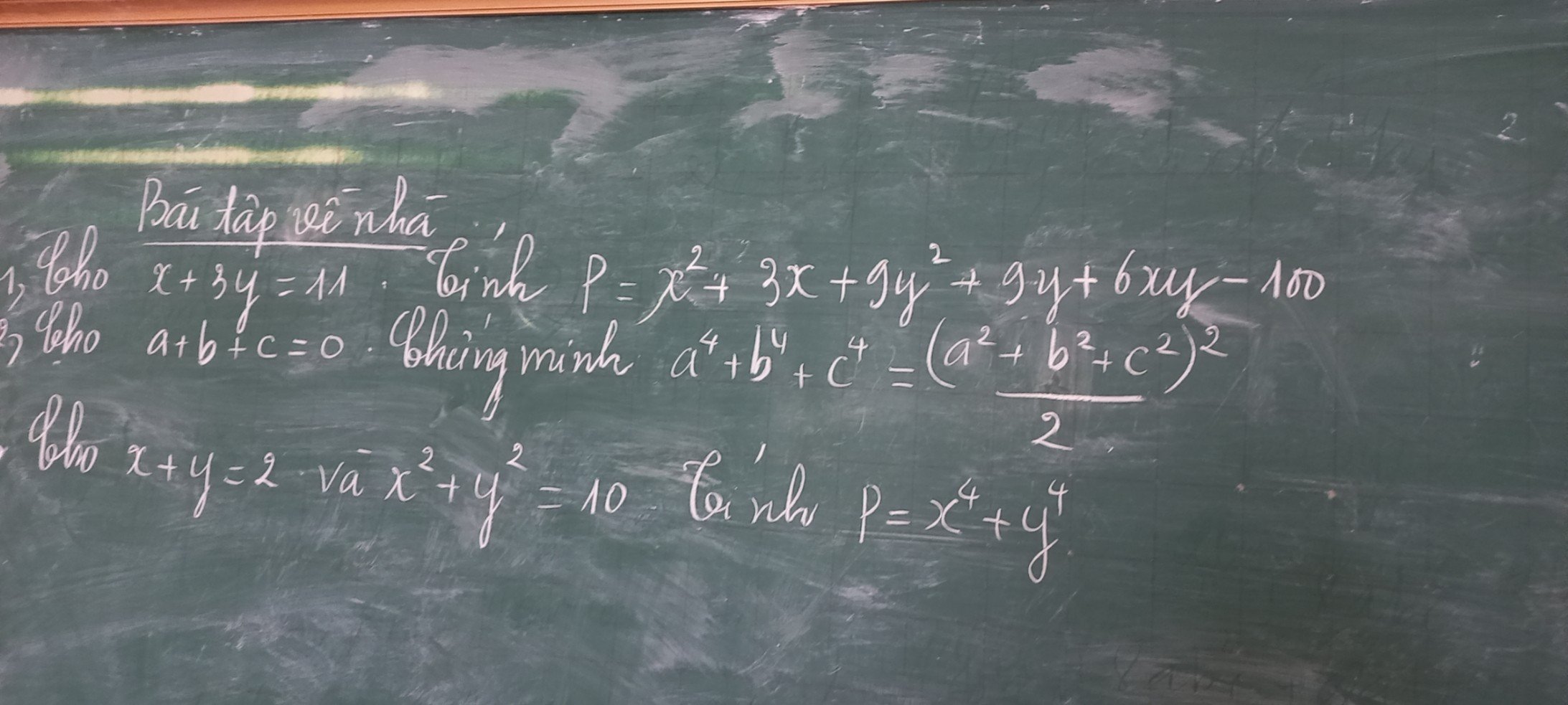1.
\(P=\left(x^2+6xy+9y^2\right)+3\left(x+3y\right)-100\)
\(=\left(x+3y\right)^2+3\left(x+3y\right)-100\)
Khi \(x+3y=11\Rightarrow P=11^2+3.11-100=54\)
3.
\(x+y=2\Rightarrow\left(x+y\right)^2=4\)
\(\Rightarrow x^2+y^2+2xy=4\)
\(\Rightarrow2xy=4-\left(x^2+y^2\right)=4-10=-6\)
\(\Rightarrow xy=-3\)
\(\Rightarrow P=\left(x^2+y^2\right)^2-2x^2y^2=10^2-2.\left(-3\right)^2=82\)
2.
\(a+b+c=0\Rightarrow\left(a+b+c\right)^2=0\)
\(\Rightarrow a^2+b^2+c^2+2ab+2bc+2ca=0\)
\(\Rightarrow a^2+b^2+c^2=-2\left(ab+bc+ca\right)\)
\(\Rightarrow\left(a^2+b^2+c^2\right)^2=4\left(ab+bc+ca\right)^2\)
\(\Rightarrow a^4+b^4+c^4+2\left(a^2b^2+b^2c^2+c^2a^2\right)=4\left(a^2b^2+b^2c^2+c^2a^2+2abc\left(a+b+c\right)\right)\)
\(\Rightarrow a^4+b^4+c^4+2\left(a^2b^2+b^2c^2+c^2a^2\right)=4\left(a^2b^2+b^2c^2+c^2a^2\right)\)
\(\Rightarrow a^4+b^4+c^4=2\left(a^2b^2+b^2c^2+c^2a^2\right)\)
\(\Rightarrow2\left(a^4+b^4+c^4\right)=a^4+b^4+c^4+2\left(a^2b^2+b^2c^2+c^2a^2\right)\)
\(\Rightarrow2\left(a^4+b^4+c^4\right)=\left(a^2+b^2+c^2\right)^2\)
\(\Rightarrow a^4+b^4+c^4=\dfrac{\left(a^2+b^2+c^2\right)^2}{2}\)