Question

Answer 1

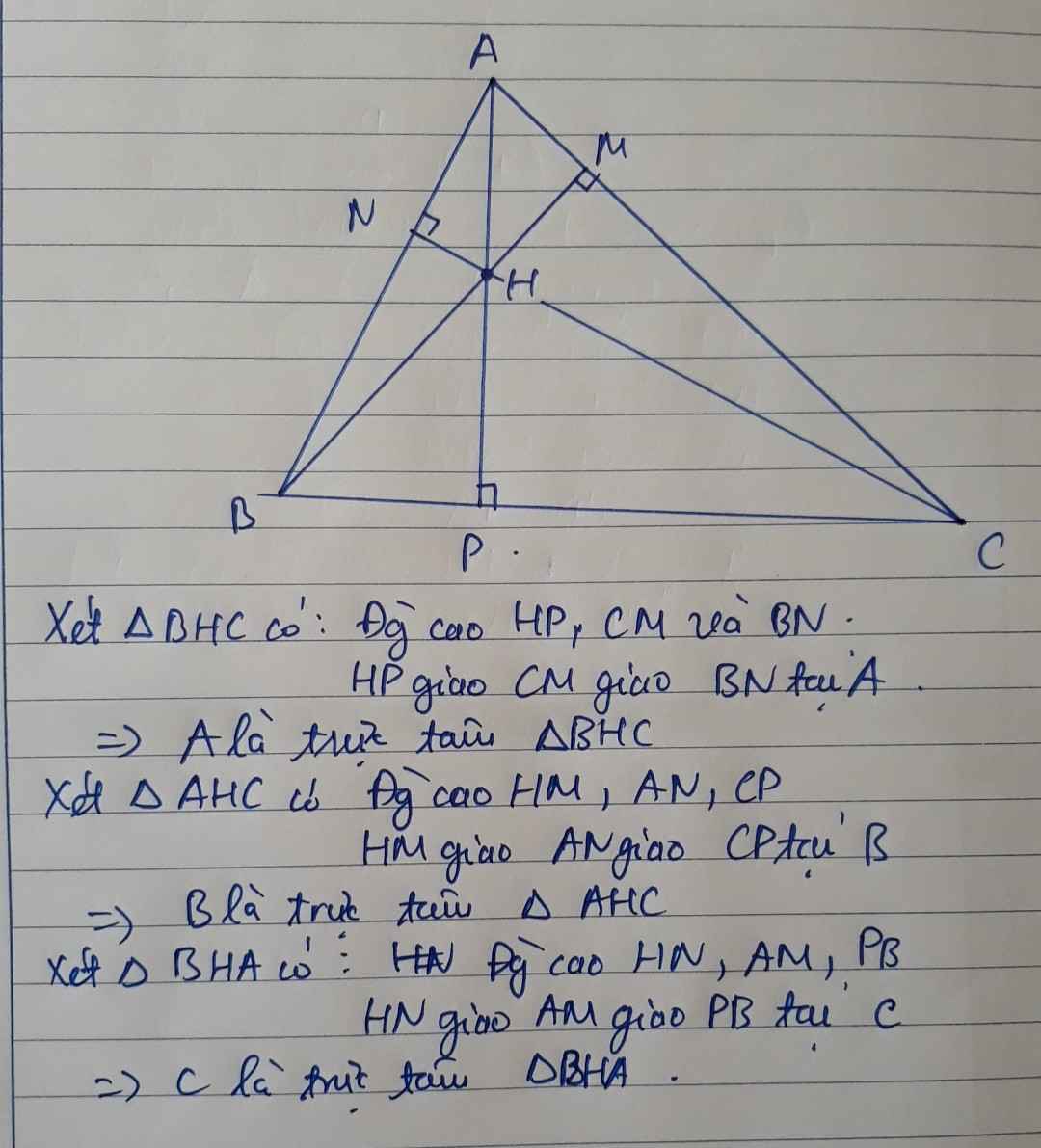
Xét ΔABC có H là trực tâm 

nên BH\(\perp\)AC tại K; CH\(\perp\)AB tại F; AH\(\perp\)BC tại F

Xét ΔHBC có

HE là đường cao ứng với cạnh BC

BF là đường cao ứng với cạnh HC

HE cắt BF tại A

Do đó: A là trực tâm của ΔHBC

Xét ΔHAC có

HK là đường cao ứng với cạnh AC

AF là đường cao ứng với cạnh HC

HK cắt AF tại B

Do đó: B là trực tâm của ΔHAC

Xét ΔHAB có

HF là đường cao ứng với cạnh AB

BE là đường cao ứng với cạnh HA

BE cắt HF tại C

Do đó: C là trực tâm của ΔHAB

Answer 2