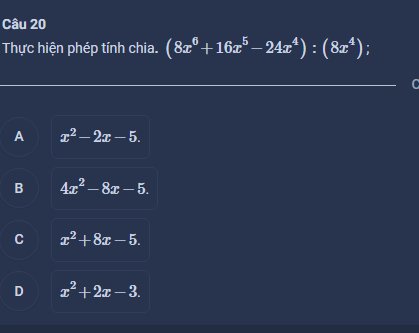
Câu 20: \(\dfrac{8x^6+16x^5-24x^4}{8x^4}=x^2+2x-3\)
=>Chọn D
Câu 19: \(\dfrac{x^4-2x^3+x^2+13x-11}{x^2-2x+3}\)
\(=\dfrac{x^4-2x^3+3x^2-2x^2+4x-6+9x-5}{x^2-2x+3}\)
\(=x^2-2+\dfrac{9x-5}{x^2-2x+3}\)
=>Chọn B
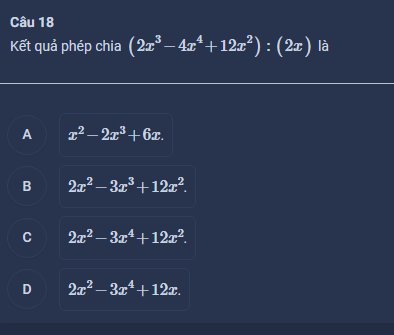
Câu 18: A
Câu 17: D
Câu 16: \(\dfrac{x^3-2x^2-x-1}{x^2+x+1}=\dfrac{x^3+x^2+x-3x^2-3x-3+x+2}{x^2+x+1}\)
\(=x-3+\dfrac{x+2}{x^2+x+1}\)
=>Thương là x-3
=>Chọn A
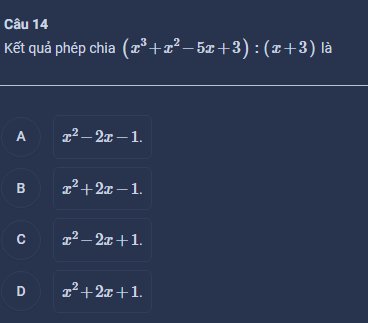
Câu 14: \(\dfrac{x^3+x^2-5x+3}{x+3}=\dfrac{x^3+3x^2-2x^2-6x+x+3}{x+3}=x^2-2x+1\)
=>Chọn C
Câu 15:
\(\dfrac{2x^3-3x^4+12x^2}{x}=\dfrac{2x^3}{x}-\dfrac{3x^4}{x}+\dfrac{12x^2}{x}=2x^2-3x^3+12x\)
=>Chọn C
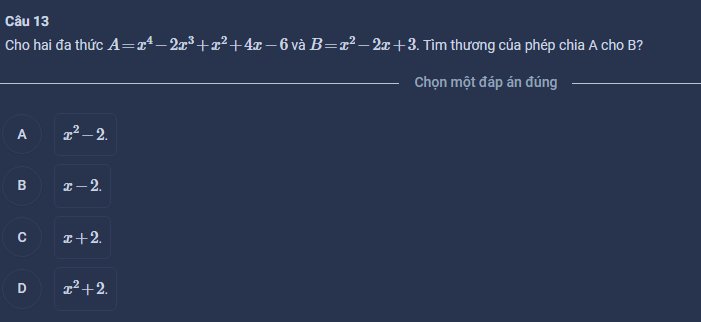
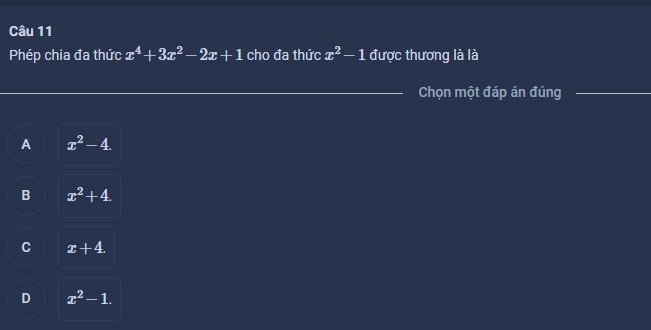
Câu 13: \(\dfrac{x^4+3x^2-2x+1}{x^2-1}=\dfrac{x^4-x^2+4x^2-4-2x+5}{x^2-1}=x^2+4+\dfrac{-2x+5}{x^2-1}\)
=>Chọn B
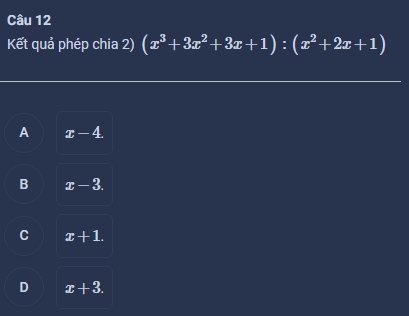
Câu 12: \(\dfrac{x^3+3x^2+3x+1}{x^2+2x+1}=\dfrac{\left(x+1\right)^3}{\left(x+1\right)^2}=x+1\)
=>Chọn C