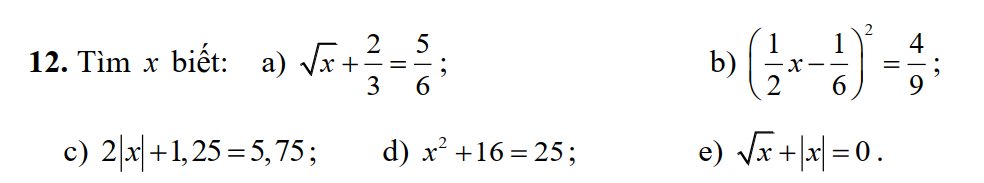a: \(\sqrt{x}+\dfrac{2}{3}=\dfrac{5}{6}\)(ĐKXĐ: x>=0)
=>\(\sqrt{x}=\dfrac{5}{6}-\dfrac{2}{3}=\dfrac{1}{6}\)
=>\(x=\left(\dfrac{1}{6}\right)^2=\dfrac{1}{36}\left(nhận\right)\)
b: \(\left(\dfrac{1}{2}x-\dfrac{1}{6}\right)^2=\dfrac{4}{9}\)
=>\(\left[{}\begin{matrix}\dfrac{1}{2}x-\dfrac{1}{6}=\dfrac{2}{3}\\\dfrac{1}{2}x-\dfrac{1}{6}=-\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x=\dfrac{2}{3}+\dfrac{1}{6}=\dfrac{5}{6}\\\dfrac{1}{2}x=-\dfrac{2}{3}+\dfrac{1}{6}=-\dfrac{3}{6}=-\dfrac{1}{2}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{5}{6}:\dfrac{1}{2}=\dfrac{5}{3}\\x=-\dfrac{1}{2}:\dfrac{1}{2}=-1\end{matrix}\right.\)
c: 2|x|+1,25=5,75
=>2|x|=5,75-1,25=4,5
=>|x|=2,25
=>\(\left[{}\begin{matrix}x=2,25\\x=-2,25\end{matrix}\right.\)
d: \(x^2+16=25\)
=>\(x^2=25-16=9\)
=>\(\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
e: ĐKXĐ: x>=0
\(\sqrt{x}+\left|x\right|=0\)
=>\(\sqrt{x}+\sqrt{x^2}=0\)
=>\(\sqrt{x}\left(\sqrt{x}+1\right)=0\)
mà \(\sqrt{x}+1>=1>0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}=0\)
=>x=0(nhận)