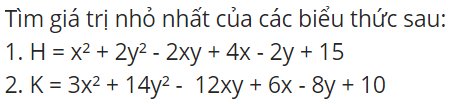1.
\(H=x^2+2y^2-2xy+4x-2y+15\\ =\left(x^2-2xy+y^2\right)+\left(4x-4y\right)+4+\left(y^2+2y+1\right)+10\\ =\left(x-y\right)^2+4\left(x-y\right)+4+\left(y+1\right)^2+10\\ =\left(x-y+2\right)^2+\left(y+1\right)^2+10\)
Ta thấy: \(\left\{{}\begin{matrix}\left(x-y+2\right)^2\ge0\forall x,y\\\left(y+1\right)^2\ge0\forall y\end{matrix}\right.\)
\(\Rightarrow\left(x-y+2\right)^2+\left(y+1\right)^2\ge0\forall x,y\\ \Rightarrow\left(x-y+2\right)^2+\left(y+1\right)^2+10\ge10\forall x,y\\ \Rightarrow H\ge10\forall x,y\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}x-y+2=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y-2=-1-2=-3\\y=-1\end{matrix}\right.\)
Vậy \(H_{min}=10\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-1\end{matrix}\right.\).
2.
\(K=3x^2+14y^2-12xy+6x-8y+10\\ =3\left[\left(x^2-4xy+4y^2\right)+\left(2x-4y\right)+1\right]+\left(2y^2+4y+2\right)+5\\ =3\left[\left(x-2y\right)^2+2\left(x-2y\right)+1\right]+2\left(y^2+2y+1\right)+5\\ =3\left(x-2y+1\right)^2+2\left(y+1\right)^2+5\)
Ta thấy: \(\left\{{}\begin{matrix}3\left(x-2y+1\right)^2\ge0\forall x,y\\2\left(y+1\right)^2\ge0\forall y\end{matrix}\right.\)
\(\Rightarrow3\left(x-2y+1\right)^2+2\left(y+1\right)^2\ge0\forall x,y\\ \Rightarrow3\left(x-2y+1\right)^2+2\left(y+1\right)^2+5\ge5\forall x,y\\ \Rightarrow K\ge5\forall x,y\)
Dấu "=" xảy ra khi: \(\left\{{}\begin{matrix}x-2y+1=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y-1=2.\left(-1\right)-1=-3\\y=-1\end{matrix}\right.\)
Vậy \(K_{min}=5\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-1\end{matrix}\right.\).
#$\mathtt{Toru}$