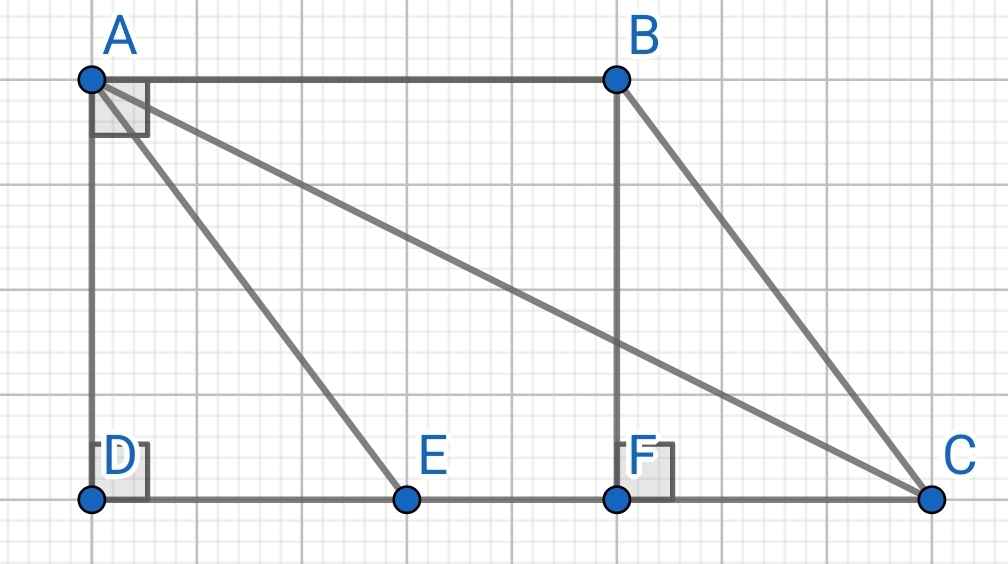
a) Do ABCD là hình thang vuông tại A có hai đáy là AB và CD (gt)
⇒ AD ⊥ CD
⇒ AD ⊥ AE
∆ADE vuông tại D
⇒ AE² = AD² + DE² (Pythagore)
= 4² + 3²
= 25
⇒ AE = 5 (cm)
b) Vẽ BF ⊥ CD tại F
ABFD có:
∠BAD = ∠ADF = ∠BFD = 90⁰
⇒ ABFD là hình chữ nhật
⇒ BF = AD = 4 (cm)
∆BFC vuông tại F
⇒ BC² = BF² + FC² (Pythagore)
⇒ FC² = BC² - BF²
= 5² - 4²
= 9
⇒ FC = 3 (cm)
⇒ DF = CD - FC
= 8 - 3
= 5 (cm)
⇒ AB = DF = 5 (cm)
CE = CD - DE
= 8 - 3
= 5 (cm)
Xét ∆ACE và ∆CAB có:
AC là cạnh chung
AE = BC = 5 (cm)
CE = AB = 5 (cm)
⇒ ∆ACE = ∆CAB (c-c-c)
⇒ ∆ACE ∽ ∆CAB (c-c-c)
c) Xét tứ giác ABCE có:
AB = CE = 5 (cm)
BC = AE = 5 (cm)
⇒ ABCE là hình bình hành (vì có các cặp cạnh đối bằng nhau)
d) AB = 5 (cm) (cmt)
Diện tích hình thang ABCD:
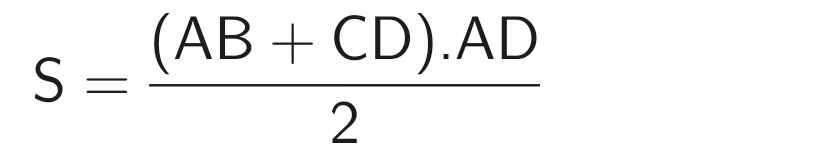
 = 26 (cm²)
= 26 (cm²)
















