Question

Answer 1

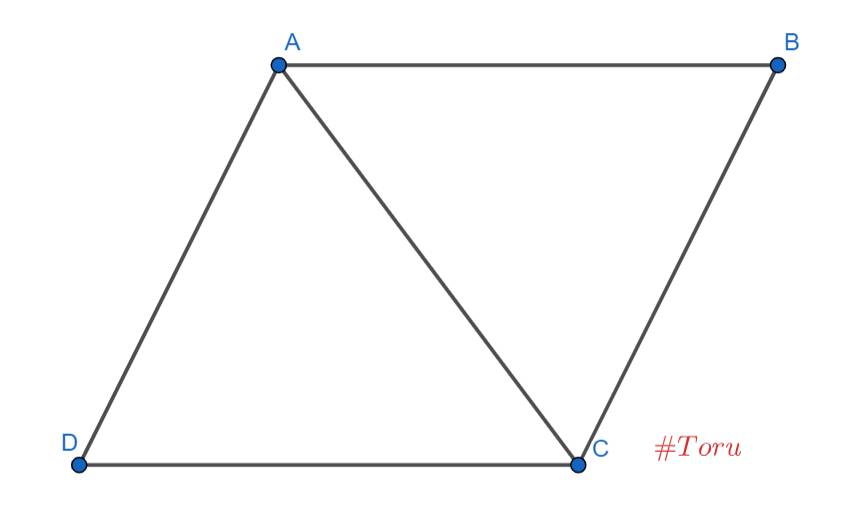
a) Vì AB // CD \(\Rightarrow\widehat{BAC}=\widehat{DCA}\) (hai góc so le trong)

Vì AD // BC \(\Rightarrow\widehat{DAC}=\widehat{BCA}\) (hai góc so le trong)

Xét \(\triangle ABC\) và \(\triangle CDA\) có: \(\left\{{}\begin{matrix}\widehat{BAC}=\widehat{DCA}\left(cmt\right)\\AC\text{ chung}\\\widehat{BCA}=\widehat{DAC}\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow\triangle ABC=\triangle CDA\left(g.c.g\right)\)

b) Vì \(\triangle ABC=\triangle CDA\left(cmt\right)\Rightarrow\left\{{}\begin{matrix}AB=CD\left(\text{hai cạnh tương ứng}\right)\\BC=DA\left(\text{hai cạnh tương ứng}\right)\end{matrix}\right.\)