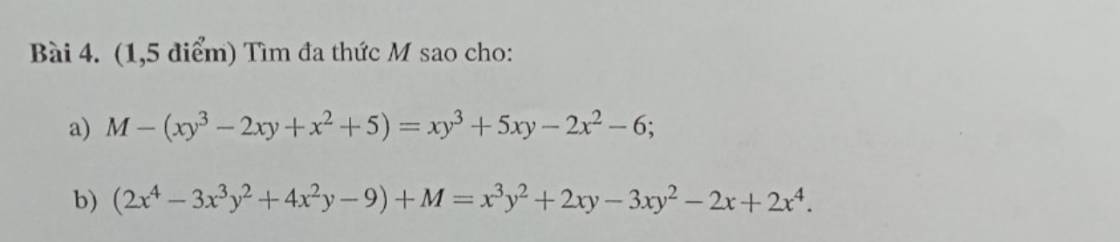a) \(M-\left(xy^3-2xy+x^2+5\right)=xy^3+5xy-2x^2-6\)
\(\Rightarrow M=xy^3+5xy-2x^2-6+\left(xy^3-2xy+x^2+5\right)\)
\(=xy^3+5xy-2x^2-6+xy^3-2xy+x^2+5\)
\(=\left(xy^3+xy^3\right)+\left(5xy-2xy\right)+\left(-2x^2+x^2\right)+\left(-6+5\right)\)
\(=2xy^3+3xy-x^2-1\)
b) \(\left(2x^4-3x^3y^2+4x^2y-9\right)+M=x^3y^2+2xy-3xy^2-2x+2x^4\)
\(\Rightarrow M=x^3y^2+2xy-3xy^2-2x+2x^4-\left(2x^4-3x^3y^2+4x^2y-9\right)\)
\(=x^3y^2+2xy-3xy^2-2x+2x^4-2x^4+3x^3y^2-4x^2y+9\)
\(=\left(x^3y^2+3x^3y^2\right)+2xy-3xy^2-2x+\left(2x^4-2x^4\right)-4x^2y+9\)
\(=4x^3y^2+2xy-3xy^2-2x-4x^2y+9\)
$\text{#}Toru$
Đúng 3
Bình luận (0)
