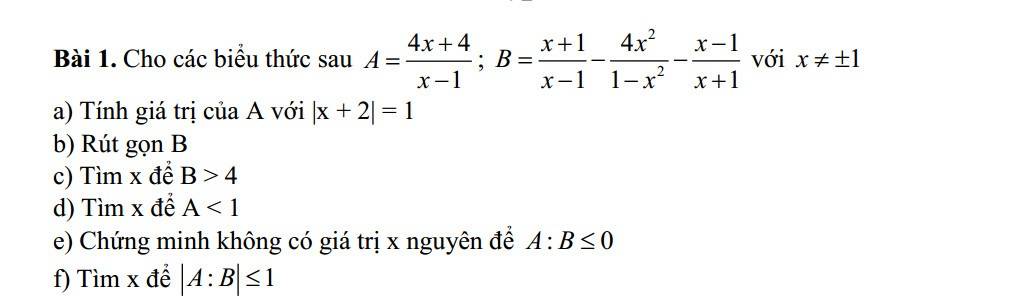a: ĐKXĐ: \(x\ne1\)
|x+2|=1
=>\(\left[{}\begin{matrix}x+2=1\\x+2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\left(nhận\right)\\x=-3\left(nhận\right)\end{matrix}\right.\)
Khi x=-1 thì \(A=\dfrac{4\left(-1+1\right)}{-1-1}=0\)
Khi x=-3 thì \(A=\dfrac{4\cdot\left(-3\right)+4}{-3-1}=\dfrac{-12+4}{-4}=2\)
b: \(B=\dfrac{x+1}{x-1}-\dfrac{4x^2}{1-x^2}-\dfrac{x-1}{x+1}\)
\(=\dfrac{x+1}{x-1}+\dfrac{4x^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{x-1}{x+1}\)
\(=\dfrac{\left(x+1\right)^2+4x^2-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+2x+1+4x^2-x^2+2x-1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{4x^2+4x}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x}{x-1}\)
c: B>4
=>\(\dfrac{4x}{x-1}>4\)
=>\(\dfrac{x}{x-1}>1\)
=>\(\dfrac{x}{x-1}-1>0\)
=>\(\dfrac{x-x+1}{x-1}>0\)
=>\(\dfrac{1}{x-1}>0\)
=>x-1>0
=>x>1
d: A<1
=>A-1<0
=>\(\dfrac{4x+4}{x-1}-1< 0\)
=>\(\dfrac{4x+4-x+1}{x-1}< 0\)
=>\(\dfrac{3x+5}{x-1}< 0\)
=>\(-\dfrac{5}{3}< x< 1\)
e: Đặt P=A:B
\(=\dfrac{4x+4}{x-1}:\dfrac{4x}{x-1}=\dfrac{4\left(x+1\right)}{x-1}\cdot\dfrac{x-1}{4x}=\dfrac{x+1}{x}\)
Để A<=0 thì \(\dfrac{x+1}{x}< =0\)
=>-1<=x<0
mà x nguyên
nên x=-1(loại)
=>Không có giá trị x nguyên nào thỏa mãn
f: |A:B|<=1
=>\(-1< =\dfrac{x+1}{x}< =1\)
=>\(\left\{{}\begin{matrix}\dfrac{x+1}{x}+1>=0\\\dfrac{x+1}{x}-1< =0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2x+1}{x}>=0\\\dfrac{1}{x}< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 0\\2x+1< =0\end{matrix}\right.\Leftrightarrow x< =-\dfrac{1}{2}\)