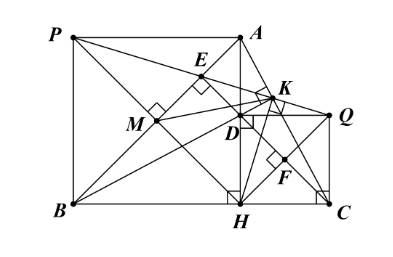
a) Ta có P là điểm đối xứng với H qua M (giả thiết).
==> M là trung điểm của PH.
Mà M cũng là trung điểm của AB (giả thiết).
Do đó tứ giác AHBP là hình bình hành (1)
∆ABH có: AH ⊥ BH và ABH=45 độ
==> ∆ABH vuông cân tại H.
Do đó AH = BH và AHB=90 độ (2)
Từ (1), (2), ta được tứ giác AHBP là hình vuông.
b) ∆ABK vuông tại K có KM là đường trung tuyến.
==> MK=1/2 AB
Mà AB = HP (do AHBP là hình vuông).
Do đó MK=1/2 HP
Vậy HP = 2MK.
c) Ta có DQ // BC (giả thiết) và DH ⊥ BC (do AH là đường cao của ∆ABC).
=> DQ ⊥ DH hay \(\widehat {HDQ} = 90^\circ \) (3)
Chứng minh tương tự, ta được HCQ=90 độ (4)
Mà DHC = 90 độ (do AH là đường cao của ∆ABC) (5)
Từ (3), (4), (5), ta được tứ giác DHCQ là hình chữ nhật.
Gọi F là giao điểm của CD và HQ.
Suy ra F là trung điểm của CD và HQ.
Do đó FD = FC = FQ = FH.
Ta có ∆DKC vuông tại K.
==> KF = FD = FC = FQ = FH.
Khi đó ∆HKQ vuông tại K.
Vì vậy HK ⊥ KQ.
Chứng minh tương tự, ta được HK ⊥ PK.
Ta có :
PKH + HKQ = 90 + 90 = 180 độ
Vậy ba điểm P, K, Q thẳng hàng.
d) Gọi E là giao điểm của CD và AB.
∆ABC có BK, AH là hai đường cao cắt nhau tại D.
==> D là trực tâm của ∆ABC.
Khi đó CD ⊥ AB tại E.
∆BCE có BCE = 180 -BEC - EBC = 180 - 90-45 = 45 độ
Suy ra DCQ = HCQ - HCD = 90 - 45 = 45 độ
Khi đó CD là tia phân giác của góc HCQ
Mà tứ giác HCQD là hình chữ nhật (cmt).
Vì vậy HCQD là hình vuông.
Tứ giác MHFE có HFD = 90 độ (HCQD là hình vuông); MEF = 90 độ (FE ⊥ AB) và EMH = 90 độ (AHBP là hình vuông).
Suy ra tứ giác MHFE là hình chữ nhật.
Khi đó EF = MH =1/2 HP và EF // MH.
∆PHQ, có: EF // PH và F là trung điểm của HQ.
Suy ra EF đi qua trung điểm của cạnh PQ.
Mà EF = MH = 1/2 HP (cmt).
Suy ra E là trung điểm của PQ.
Khi đó ba điểm P, E, Q thẳng hàng.
Vậy các đường thẳng CD, AB và PQ đồng quy tại E.
đề ko khó mấy mà =) có cái này hay lắm nè Khánh





















